简介
xgboost(Extreme Gradient Boosting)是一款常用的机器学习框架,其诞生于2014年12月,因具有良好的学习效果以及高效的训练速度得到广泛关注。仅在2015年,在Kaggle竞赛中获胜的29个算法中,有17个使用了XGBoost库,而作为对比,近年大热的深度神经网络方法,这一数据则是11个。在KDDCup 2015竞赛中,排名前十的队伍全部使用了XGBoost库。XGBoost不仅学习效果很好,而且速度也很快,相比梯度提升算法在另一个常用机器学习库scikit-learn中的实现,XGBoost的性能经常有十倍以上的提升。
xgboost与另一种ensemble模型gbdt(Gradient boosting decision tree)有着紧密的联系,两者均与决策树、提升模型、梯度提升等概念相关。本文从决策树出发,逐步进行xgboost推导,并结合实例分析手动计算过程,最终给出代码实现,希望有助于大家理解xgboost相关原理。
决策树(Decision Tree)
决策树是传统机器学习中常见的一种模型,其易于理解,可解释性强,计算速度快。
分类决策树
构建分类决策树模型的过程中最关键的步骤在于如何选择结点分裂准则,常见的分裂准则有ID3、C4.5等,相关概念可参考决策树。
CART
CART模型是决策树中比较特殊的一种模型,其既可以用于分类又可以用于回归预测,分类树采用基尼指数最小化准则,回归采用平方误差最小化准备,相关概念可参考CART-分类与回归树。
提升树(Boosting Tree)
提升方法(boosting)
提升方法的思想:对于一个复杂任务来说,将多个专家系统的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好,简而言之就是“三个臭皮匠顶个诸葛亮”的道理。
对于分类问题而言,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)要求比精确的分类规则(强分类器)容易得多。提升方法就是从弱学习算法出发,反复学习,得到一系列弱分类器,然后组合这些弱分类器,构成一个强分类器。
加法模型
加法模型表示如下
$$f(x)=\sum_{m=1}^{M}\beta_mb(x;\gamma_m)$$
其中$b(x;\gamma_m)$为基函数,$\gamma_m$为基函数的参数,$\beta_mb$为基函数的系数。
- 注:傅立叶变换可以看成一种加法模型
前向分布算法
在给定训练数据和损失函数$L(y,f(x))$的情况下,学习加法模型$f(x)$成为经验风险极小化问题:
$$\mathop{min}_{\beta_m,\gamma_m}\sum_{i=1}^{N}L[y_i,\sum_{m=1}^{M}\beta_mb(x_i;\gamma_m)]$$
使用前向分布算法解决这一优化问题的思路是:因为学习的是加法模型,如何能够从前向后,每一步只学习一个基函数及其系数,逐步逼近优化目标函数,就可以简化优化的复杂度。具体地,只需优化如下损失函数:
$$\mathop{min}_{\beta,\gamma}\sum_{i=1}^{N}L(y_i,\beta b(x_i;\gamma))$$
提升树模型
以决策树为基函数的提升方法称为提升树。提升树模型可以表示为决策树的加法模型
$$f_M(x)=\sum_{m=1}^{M}T(x,\Theta_m)$$
其中$T(x,\Theta_m)$表示决策树,$\Theta_m$表示决策树的参数, $M$表示决策树的个数。对于分类问题决策树采用二叉分类树,对于回归问题决策树采用二叉回归树。
前向回归算法:
$$
\begin{split}
f_0(x) &= 0 \\
f_m(x) &= f_{m-1}(x)+T(x;\Theta_m),\quad m=1,2,…,M \\
f_M(x) &= \sum_{m=1}^{M}T(x;\Theta_m)
\end{split}
$$
给定当前模型$f_{m-1}(x)$,需求解,
$$
\hat \Theta_m=\mathop{\arg\min}_{\Theta_m}\sum_{i=1}^{N}L(y_i,f_{m-1}(x_i)+T(x;\Theta_m))
$$
得到$\hat \Theta_m$即,第$m$棵树的参数。
当使用平方误差损失函数的时候,
$$L(y,f(x))=(y-f(x))^2$$
其损失变为
$$
\begin{split}
L(y,f_{m-1}(x)+T_m(x;\Theta))&=[y-f_{m-1}(x) - T_m(x;\Theta)]^2\\
&=[r-T_m(x;\Theta)]^2
\end{split}
$$
其中$r=y-f_{m-1}(x)$就是当前拟合数据的残差。所以对于回归问题(回归问题的损失函数一般为MSE)的提升树算法来说,只需要简单拟合当前模型的残差。
梯度提升决策树(GBDT)
提升树利用加法模型与前向分布算法实现学习的优化过程,当损失函数是平方损失函数时,每一步优化比较简单。但对于一般损失函数而言,往往每一步优化并不那么容易,所以需要寻找其他方式求解。
损失函数如下
$$
L(\Theta_m)=\sum_{i=1}^{N}L(y_i,f_{m-1}(x_i)+T(x;\Theta_m))
\tag{4.1}
$$
我们的目的是让4.1式最小,尝试用泰勒一阶展开有
$$
L(\Theta_m) \approx \sum_{i=1}^{N}[L(y_i,f_{m-1}(x_i)) + \frac{\partial{L(y_i,f_{m-1}(x_i))}}{\partial{L(f_{m-1}(x_i))}} \cdot T(x;\Theta_m)]
\tag{4.2}
$$
- 注: 泰勒一阶展开公式$f(x+\Delta x)=f(x) + \frac{\partial f(x)}{\partial x} \cdot \Delta x$
由于迭代后损失函数减小,所以
$$
L(\Theta_m)- \sum_{i=1}^{N}L(y_i,f_{m-1}(x_i))<0
$$
即
$$
\sum_{i=1}^{N}[\frac{\partial{L(y_i,f_{m-1}(x_i))}}{\partial{L(f_{m-1}(x_i))}} \cdot T(x;\Theta_m)]<0
\tag{4.3}
$$
如果让提升树$T(x;\Theta_m)$每次拟合$L(y_i,f_{m-1}(x_i))$的负梯度
$$
T(x;\Theta_m)=-\frac{\partial{L(y_i,f_{m-1}(x_i))}}{\partial{L(f_{m-1}(x_i))}}
\tag{4.4}
$$
可以保证4.3式始终小于0。
例子
训练数据如下表所示,$x$的取值范围为区间$[0.5,10.5]$,$y$的取值范围为区间$[5.0,10.0]$,使用GBDT算法解决该回归问题。
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 5.56 | 5.7 | 5.91 | 6.4 | 6.8 | 7.05 | 8.9 | 8.7 | 9 | 9.05 |
回归问题的损失函数使用平方误差损失函数,所以该问题退化为使用回归树拟合残差。
- 求解第一棵回归树
由于只有$x$一个变量,因此最优切分变量为$x$。接下来假设9个切分点为$[1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5]$,计算每个切分点的输出值。如$s=1.5$时,$R_1={1},R_2={2,3,4,5,6,7,8,9,10}$,这两个区域的输出值分别为$c_1=5.56,c_2=\frac{1}{9}(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.50$,所以有
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| $c_1$ | 5.56 | 5.63 | 5.72 | 5.89 | 6.07 | 6.24 | 6.62 | 6.88 | 7.11 |
| $c_2$ | 7.5 | 7.73 | 7.99 | 8.25 | 8.54 | 8.91 | 8.92 | 9.03 | 9.05 |
接下来计算每个切分点的误差,如$s=1.5$时,$loss(s=1.5)=\frac{1}{2}(5.56-5.56)^2+\sum_{i=2}^{10}\frac{1}{2}(y_i-7.5)^2=0+15.72=15.72$,所以有
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| $loss(s)$ | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
其中当$s=6.5$时,$loss(s)$最小,因此第一个划分变量是$j=x,s=6.5$。所以回归树为
$$
T_1(x) = \begin{cases}
6.24\quad x \lt 6.5 \\
8.91 \quad x \geq 6.5 \\
\end{cases}
$$
$$ f_1(x) = T_1(x)$$
残差为$r_{2i}= y_i - f_1(x)$,如下
| $x_i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $r_{2i}$ | -0.68 | -0.54 | -0.33 | 0.16 | 0.56 | 0.81 | -0.01 | -0.21 | 0.09 | 0.14 |
$$L(y,f_1(x)) = \sum_{i=1}^{10}(y_i-f_1(x))^2=1.93$$
- 接下来对上一步残差进行拟合
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| $c_1$ | -0.68 | -0.61 | -0.52 | -0.35 | -0.17 | -0.003 | -0.004 | -0.03 | -0.02 |
| $c_2$ | 0.07 | 0.15 | 0.22 | 0.23 | 0.164 | 0.003 | 0.01 | 0.12 | 0.14 |
| $loss(s)$ | 0.71 | 0.50 | 0.40 | 0.56 | 0.83 | 0.97 | 0.97 | 0.95 | 0.95 |
其中当$s=3.5$时,$loss(s)$最小,因此第一个划分变量是$j=x,s=3.5$。
所以回归树为
$$
T_2(x) = \begin{cases}
-0.52\quad x \lt 3.5 \\
0.22 \quad x \geq 3.5 \\
\end{cases}
$$
$$ f_2(x) = f_1(x)+T_2(x) = \begin{cases}
5.72\quad x \lt 3.5 \\
6.46 \quad 3.5 \le x \lt 6.5 \\
9.13 \quad x \ge 6.5 \\
\end{cases} $$
用$f_2(x)$拟合训练数据的平方损失误差是
$$L(y,f_2(x)) = \sum_{i=1}^{10}(y_i-f_2(x))^2=0.79$$
假设此时损失函数满足要求,则最终的提升树为
$$
f(x) = f_2(x)=
\begin{cases}
5.72\quad x \lt 3.5 \\
6.46 \quad 0.5 \le x \lt 6.5 \\
9.13 \quad x \ge 6.5 \\
\end{cases}
$$
xgboost
xgboost的损失函数与gbdt有所不同,其形式如下
$$
L(\Theta_m)=\sum_{i=1}^{N}L(y_i,f_{m-1}(x_i)+T(x;\Theta_m)) + \Omega(T(x;\Theta_m))+ C
\tag{5.1}
$$
其中$i$是指地$i$个样本,$f_{m-1}(x_i)$表示第$m-1$个模型对样本$i$的预测值,$T(x;\Theta_m)$表示第$m$个树模型,$\Omega(T(x;\Theta_m)$表示正则项,$C$表示计算过程中的一些常数项。
对5.1式连加部分尝试用泰勒二阶展开有
$$
L(\Theta_m) \approx \sum_{i=1}^{N}[L(y_i,f_{m-1}(x_i)) + \frac{\partial{L(y_i,f_{m-1}(x_i))}}{\partial{L(f_{m-1}(x_i))}} \cdot T(x;\Theta_m) + \frac{1}{2} \cdot \frac{\partial^2{L(y_i,f_{m-1}(x_i))}}{\partial{L(f_{m-1}(x_i))^2}} \cdot T^2(x;\Theta_m)]+ \Omega(T(x;\Theta_m)) + C
\tag{5.2}
$$
- 注: 泰勒二阶展开式$f(x+\Delta x)=f(x) + \frac{\partial f(x)}{\partial x} \cdot \Delta x + \frac{\partial^2 f(x)}{\partial^2 x} \cdot \Delta^2 x$
此处定义样本$i$的一阶和二阶导数为
$$
g_i=\frac{\partial{L(y_i,f_{m-1}(x_i))}}{\partial{L(f_{m-1}(x_i))}} \\
h_i=\frac{\partial^2{L(y_i,f_{m-1}(x_i))}}{\partial{L(f_{m-1}(x_i))^2}}
$$
所以5.1式可以表示为
$$
L(\Theta_m) \approx \sum_{i=1}^{N}[L(y_i,f_{m-1}(x_i)) + g_i \cdot T(x;\Theta_m) + \frac{1}{2} \cdot h_i \cdot T^2(x;\Theta_m)]+ \Omega(T(x;\Theta_m)) + C
\tag{5.3}
$$
其中$\sum_{i=1}^{N}L(y_i,f_{m-1}(x_i))$是定值可以和$C$项合并,有
$$
L(\Theta_m) \approx \sum_{i=1}^{N}[g_i \cdot T(x;\Theta_m) + \frac{1}{2} \cdot h_i \cdot T^2(x;\Theta_m)]+ \Omega(T(x;\Theta_m)) + C
\tag{5.4}
$$
决策树的正则项一般考虑的是叶子结点的个数和叶子权值,比较常见的正则项如下
$$
\Omega(T(x;\Theta_m)) = \gamma \cdot T_t+\lambda \cdot \frac{1}{2}\sum_{j=1}^{T}w^2_j
$$
5.4式变为
$$
L(\Theta_m) \approx \sum_{i=1}^{N}[g_i \cdot T(x;\Theta_m) + \frac{1}{2} \cdot h_i \cdot T^2(x;\Theta_m)]+ \gamma \cdot T_t+\lambda \cdot \frac{1}{2}\sum_{j=1}^{T}w^2_j + C
\tag{5.5}
$$
为了进一步整合3式,对$T(x;\Theta_m)$的表达形式进行修改,$T(x;\Theta_m)$重新定义为
$$
T(x;\Theta_m)=w_{q(x)}
$$
其中$w$是叶子结点的权重值,$q$函数表示输入$x$和叶子结点的对应关系。所以5.5式变为
$$
L(\Theta_m) \approx \sum_{i=1}^{N}[g_i \cdot w_{q(x_i)} + \frac{1}{2} \cdot h_i \cdot w^2_{q(x_i)}]+ \gamma \cdot T_t+\lambda \cdot \frac{1}{2}\sum_{j=1}^{T}w^2_{q(x_i)} + C
\tag{5.6}
$$
对5.6式做进一步推导,$\sum_{i=1}^{N}[g_i \cdot w_{j}(x_i)]$表示第$m$棵树的输出的乘积,这是从样本角度来看的;从树的角度来看,每个样本一定且唯一被分到其中的一个叶子结点,一个叶子结点可以分到多个样本,可以将每个叶子结点的样本梯度相加,再乘以叶子结点的权值,最后对所有叶子结点求和,所以有
$$
\sum_{i=1}^{N}g_i \cdot w_{q(x_i)}=\sum_{j=1}^{T}(\sum_{i \in I_j}g_i)w_{j} \\
\sum_{i=1}^{N}h_i \cdot w^2_{q(x_i)}=\sum_{j=1}^{T}(\sum_{i \in I_j}h_i)w^2_{j}
$$
把位于同一叶子上的一阶偏导和记做$G$,同一叶子上的二阶偏导和记为$H$,所以最终1式变为
$$
\begin{split}
L(\Theta_m) &\approx \sum_{j=1}^{T}[(\sum_{i \in I_j}g_i)w_{j}+ \frac{1}{2} \cdot (\sum_{i \in I_j}h_i)w^2_{j}]+ \gamma \cdot T_t+\lambda*\frac{1}{2}\sum_{j=1}^{T}w^2_{j} + C \\
&\approx \sum_{j=1}^{T}[G_i \cdot w_{j}+ \frac{1}{2} \cdot (\lambda+ H_i )w^2_{j}]+ \gamma \cdot T_t + C
\end{split}
\tag{5.7}
$$
5.7式对$w_mj$求偏导令其为0,有
$$
\begin{split}
\frac{\partial L(\Theta_m)}{\partial w_{mj}}=0 =>\\
G_j+(H_j+\lambda)=0 =>\\
w_{j}=-\frac{G_j}{H_j+\lambda}
\end{split}
$$
然后带回公式7有
$$
L(\Theta_m) \approx -\frac{1}{2}\sum_{j=1}^{T}\frac{G^2_j}{H_j+\lambda} + \gamma \cdot T_t
\tag{5.8}
$$
公式5.8就是最终的损失函数。
该损失函数怎么使用呢?其实它可以指导建树,建树的时候最关键的一步就是选择一个分裂的准则,也就如何评价分裂的质量。比如在上面GBDT的介绍里,选择MSE来评价分裂的质量。在xgboost里分裂准则直接与损失函数挂钩,具体来说是通过损失函数计算增益$Gain$
$$
Gain=\frac{1}{2}[\frac{G^2_L}{H_L+\lambda}+\frac{G^2_R}{H_R+\lambda}-\frac{(G_L+G_R)^2}{(H_L+H_R)+\lambda}] - \gamma
$$
其中$ \frac{(G_L+G_R)^2}{(H_L+H_R)+\lambda}$表示对于一个结点,如果不分裂的话此时的损失。如果在这个节点进行分裂,则分裂后的左右子结点的损失分别为$\frac{G^2_L}{H_L+\lambda}$,$\frac{G^2_R}{H_R+\lambda}$,找到一种分裂使$Gain$最大。
示例
数据集如下,15条样本数据,2个特征:
| ID | $x_1$ | $x_2$ | y |
|---|---|---|---|
| 1 | 1 | -5 | 0 |
| 2 | 2 | 5 | 0 |
| 3 | 3 | -2 | 1 |
| 4 | 1 | 2 | 1 |
| 5 | 2 | 0 | 1 |
| 6 | 6 | -5 | 1 |
| 7 | 7 | 5 | 1 |
| 8 | 6 | -2 | 0 |
| 9 | 7 | 2 | 0 |
| 10 | 6 | 0 | 1 |
| 11 | 8 | -5 | 1 |
| 12 | 9 | 5 | 1 |
| 13 | 10 | -2 | 0 |
| 14 | 8 | 2 | 0 |
| 15 | 9 | 0 | 1 |
参数设置:树的深度设置为3,棵树设置为2,学习率设置为0.1,两个正则参数$\lambda=1,\gamma=0$。分类问题,损失函数选择logloss。
下面计算logloss的一阶导数和二阶导数,假设预测值为$\hat{y_i}$。
$$
L(y_i,\hat{y_i})=-y_ilog(y_{i,pred}) - (1-y_i)log(1-y_{i,pred})
$$
其中$y_{i,pred}=\frac{1}{1+e^{-\hat{y_i}}}$
一阶导数
$$
L’(y_i,\hat{y_i})=(\frac{y_i}{y_{i,pred}}-\frac{1-y_i}{1-y_{i,pred}})y^{‘}_{i,pred}=\frac{y_i-y_{i,pred}}{y_{i,pred}(1-y_{i,pred})}*y_{i,pred}(1-y_{i,pred})=y_i-y_{i,pred}
$$
二阶导数
$$
L’’(y_i,\hat{y_i})=(y_i-y_{i,pred})’=-y_{i,pred}(1-y_{i,pred})
$$
设置初始预测值$y_{i,pred}=0.5$,举例计算$ID_1$样本的一阶二阶导数。
$g_1=y_i-y_{i,pred}=0-0.5=-0.5$
$h_1=-y_{i,pred}(1-y_{i,pred})=-0.5*(1-0.5)=-0.25$
所以有
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $g_i$ | 0.5 | 0.5 | -0.5 | -0.5 | -0.5 | -0.5 | -0.5 | 0.5 | 0.5 | -0.5 | -0.5 | -0.5 | 0.5 | 0.5 | -0.5 |
| $h_i$ | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
进行结点分裂。首先看特征$x_1$,其取值为$[1,2,3,6,7,8,9,10]$,需要依次计算每个取值进行分裂的增益。
以取值1为划分时
左结点样本$I_L=[]$,右结点样$I_L=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]$
左结点为空,所以$G_L=0$,$H_L=0$
右结点一阶导数和为$G_R=\sum_{i \in I_R}g_i=-1.5$,二阶导数和为$H_R=\sum_{i \in I_R} h_i=3.75$
所以增益$Gain=0$。
以取值2为划分时
左结点样本$I_L=[1,4]$,右结点样$I_L=[2,3,5,6,7,8,9,10,11,12,13,14,15]$
左结一阶导数和为$G_L=\sum_{i \in I_L}g_i=0.5-0.5=0$,二阶导数和为$H_L=\sum_{i \in I_L} h_i=0.25+0.25=0.5$
右结点一阶导数和为$G_R=\sum_{i \in I_R}g_i=0.5-0.5+…+0.5-0.5=-1.5$,二阶导数和为$H_R=\sum_{i \in I_R} h_i=0.25+…+0.25=3.25$
所以增益为
$$
\begin{split}
Gain&=[\frac{G^{2}_{L}}{H_{L}+\lambda}+\frac{G^{2}_{R}}{H_{R}+\lambda}-\frac{(G_{L}+G_{R})^2}{(H_{L}+H_{R})+\lambda}]\\
&=[0+\frac{1.5^2}{(-3.25)+1}-\frac{(0+1.5)^2}{(-0.5-3.25)+1}]\\
&=0.0557275541796
\end{split}
$$
所以有
| split_point | 2 | 3 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|
| $G_L$ | 0 | 0 | -0.5 | -1 | -1 | -1 | 2 |
| $H_L$ | 0.5 | 1 | 1.25 | 2 | 2.5 | 3 | 3.5 |
| $G_R$ | -1.5 | -1.5 | -1 | -0.5 | -0.5 | -0.5 | 0.5 |
| $H_R$ | 3.25 | 2.75 | 2.5 | 1.75 | 1.25 | 0.75 | 0.25 |
| $Gain$ | 0.0557 | 0.1263 | -0.0769 | -0.0494 | -0.0769 | -0.0808 | 0.6152 |
特征$x1$以$x1<10$分裂时可以得到最大的增益0.615204678363。
看特征$x_2$,其取值为$[-5,-2,0,2,5]$,需要依次计算每个取值进行分裂的增益。
| split_point | -2 | 0 | 2 | 5 |
|---|---|---|---|---|
| $G_L$ | -0.5 | 0 | -1.5 | -1 |
| $H_L$ | 0.75 | 1.5 | 2.25 | 3 |
| $G_R$ | -1 | -1.5 | 0 | -0.5 |
| $H_R$ | 3 | 2.25 | 1.5 | 0.75 |
| $Gain$ | -0.0808 | 0.2186 | 0.2186 | -0.0808 |
以特征$x_2$分裂,最大的增益是0.218623481781,小于以$x_1$分裂的增益,所以第一次分裂以$x_1<10$进行分裂。
由于设置的最大深度是3,此时只有1层,所以还需要继续往下分裂。
左子节点的样本集合$I_L=[1,2,3,4,5,6,7,8,9,10,11,12,14,15] $
右子节点的样本集合$I_R=[13]$
右子结点只剩下一个样本,不需要再进行分裂,可以计算结点值
$$
w=-\frac{G_R}{H_R+\lambda}=-\frac{0.5}{1+0.25}=-0.4
$$
下面对左子结点$I_L=[1,2,3,4,5,6,7,8,9,10,11,12,14,15]$进行分裂,分裂的时候把此时的结点看成根节点,同样也是需要遍历所有特征(x1,x2)的所有取值作为分裂点,选取增益最大的点。
遍历$x_1$
| split_point | 2 | 3 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| $G_L$ | 0 | 0 | -0.5 | -1 | -1 | -1 |
| $H_L$ | 0.5 | 1 | 1.25 | 2 | 2.5 | 3 |
| $G_R$ | -2 | -2 | -1.5 | -1 | -1 | -1 |
| $H_R$ | 3 | 2.5 | 2.25 | 1.5 | 1 | 0.5 |
| $Gain$ | 0.1111 | 0.2540 | -0.0855 | -0.1556 | -0.1032 | 0.0278 |
可以发现$x_1$在$x<3$时能取得最大增益0.253968253968。
遍历$x_2$
| split_point | -2 | 0 | 2 | 5 |
|---|---|---|---|---|
| $G_L$ | -0.5 | -0.5 | -2 | -1.5 |
| $H_L$ | 0.75 | 1.25 | 2 | 2.75 |
| $G_R$ | -1.5 | -1.5 | 0 | -0.5 |
| $H_R$ | 2.75 | 2.25 | 1.5 | 0.75 |
| $Gain$ | -0.1460 | -0.0855 | 0.4444 | -0.1460 |
可以发现$x_2$在$x<2$时能取得最大增益0.4444。
综上本次分裂应该选择$x<2$作为分裂点,分裂后左右子结点集合如下
左子节点的样本集合$I_L=[1,3,5,6,8,10,11,15] $
右子节点的样本集合$I_R=[2,4,7,9,12,14]$
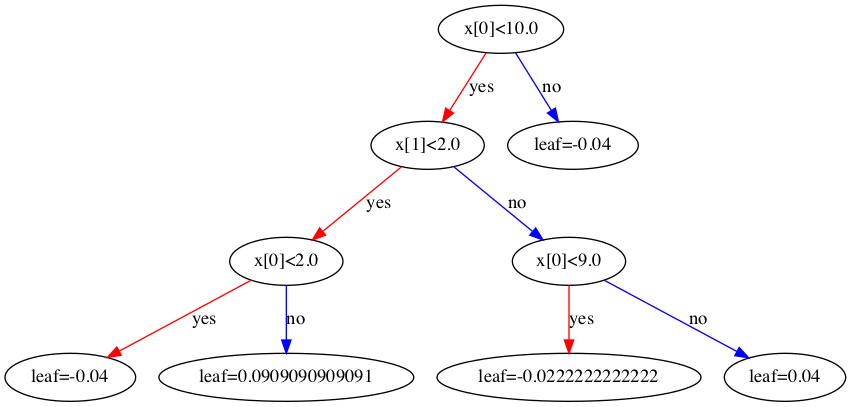
到此为止,第一棵树构建完毕,下面给出表达形式。根据加法模型,第一棵树的预测结果应该为
$$y=f_0(x_i)+f_1(x_i)$$
其中$f_0(x_i)$是初始值,可以看成第0棵树。在第1步中,我们假设初始值$y_{i,pred}$=0.5,由于使用logloss损失函数,所以其原始输出需要进行一个sigmoid的反变换$f_0=ln(\frac{0.5}{1-0.5})=0$,所以第一棵树的预测结果就是
$$y=f_0(x_i)+f_1(x_i)=0+w_{q(x_i)}=w_{q(x_i)}$$
第一棵树的结构如下图
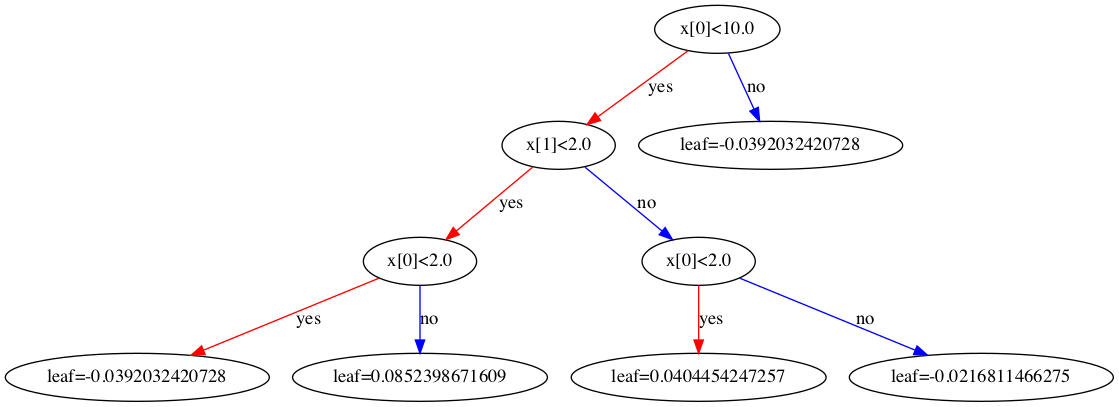
建立第2棵树,整个过程和第1棵树一样,但是需要更新$y_{i,pred}$,也就是说在第一棵树的基础上进行第二棵树的构建,这里的思想和GBDT一致。
以ID=1样本为例,更新$y_{i,pred}$。对于ID=1经过第一棵树,落在-0.04结点,经过sigmoid映射后的值为$p_{1,pred}=\frac{1}{1+e^{0.04}}=0.490001$,所以有
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $y_{i,pred}$ | 0.49 | 0.49 | 0.52 | 0.49 | 0.52 | 0.52 | 0.49 | 0.52 | 0.49 | 0.52 | 0.52 | 0.51 | 0.49 | 0.49 | 0.52 |
| $g_i$ | 0.49 | 0.49 | -0.48 | -0.51 | -0.48 | -0.48 | -0.51 | 0.52 | 0.49 | -0.48 | -0.48 | -0.49 | 0.49 | 0.49 | -0.48 |
| $h_i$ | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
根据上表可推导出第二棵树的结构如下图
- 注: 由于hexo排版问题,表格中的数据进行了截位处理,可能精度不够,可以使用下面的程序进行计算。
代码
针对上面的例子,简单实现了xgboost的求解过程,代码如下
1 | # coding=utf-8 |
代码详见xgboost简单实现
参考
- 机器学习实战,人民邮电出版社
- 统计学习方法,清华大学出版社
- xgboost原理分析以及实践
- XGBoost Documentation