决策树(decision tree)是一种多功能的机器学习算法,它可以实现分类和回归任务,同时也是随机森林的重要组成部分,本篇博客主要讨论用于分类的决策树。
分类型决策树是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内结点表示一个特征,叶子结点表示一个类别。
相关数学概念
信息熵
在将实例分配到子结点的过程中需要选择一个度量条件来判断该实例属于哪个子结点,常见的方法是用信息熵作为度量条件。
在信息论中,熵(entropy)表示随机变量不确定性的度量,设$X$是一个取有限个值的离散随机变量,其概率分布为
$$P(X=x_i)=p_i, i=1,2,…,n$$
则随机变量$X$的熵的定义为
$$
H(X)=-\sum_{i=1}^{n}p_ilog_{2}p_i
\tag{1}
$$
若$p_i=0$,则定义$0log0=0$。熵越大,说明随机变量的不确定性越大。
条件熵
设有随机变量(X,Y),其联合概率分布为
$$P(X=x_i,Y=y_i)=p_{ij}, i=1,2,…,n;j=1,2,…,m$$
条件熵H(Y|X)表示在已知随机变量$X$的条件下随机变量$Y$的不确定性。随机变量$X$给定的条件下随机变量$Y$的条件熵H(Y|X),定义为$X$给定条件下$Y$的条件概率分布的熵对$X$的数学期望。
$$P(Y|X)=\sum_{i=1}^{n}p_iH(Y|X=x_i)$$
其中$p_i=P(X=x_i)$
当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时,所对应的熵和条件熵分别称为经验熵(empirical entropy)和经验条件熵(empirical conditional entropy).
信息增益
信息增益(information gain)表示得知特征$X$的信息而使得类别$Y$的信息不确定性减少的程度。
特征A对训练数据集D的信息增益$g(D,A)$,定义为集合D的经验熵$H(D)$与特征A给定的条件下D的经验条件熵$H(D|A)$之差,即
$$g(D,A)=H(D)-H(D|A)$$
一般地,熵$H(Y)$与条件熵$H(Y|X)$之差称为互信息,决策树中的信息增益等价于训练数据集中类别和特征的互信息。
信息增益比
特征A对训练数据集D的信息增益比$g_R(D,A)$定义为其信息增益$g(D,A)$与训练数据集$D$的经验熵$H(D)$之比
$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$
原理
决策树在建模过程中使用信息增益准则选择特征,给定训练集$D$和特征$A$,经验熵$H(D)$表示对数据集$D$进行分类的不确定性。而经验条件熵$H(D|A)$表示在特征$A$给定的条件下对数据集$D$进行分类的不确定性,它们的差即信息增益,表示由于特征$A$而使得对数据集$D$的分类的不确定性减少的程度。显然,对于数据集$D$而言,信息增益依赖于特征,不同的特征具有不同的信息增益,信息增益大的特征具有更强的分类能力。
根据信息增益准则的特征选择方法是:对训练数据集$D$,计算其每个特征的信息增益,并比较它们的大小,选择信息增益大的特征。
ID3算法
设训练数据集为$D$,$|D|$表示其样本容量,即样本个数。设有$K$个类$C_k,k=1,2,…,K$,$|C_k|$为属于$C_k$的样本个数,$\sum_{k=1}^{K}|C_k|=|D|$。设特征$A$有$n$个不同的取值${a_1,a_2,…,a_n}$,根据特征$A$的取值将$D$划分为n个子集$D_1,D_2,…,D_n$,$|D_i|$为$D_i$的样本个数,$\sum_{k=1}^{n}|D_i|=|D|$。记子集$D_i$中属于类$C_k$的样本的集合为$D_{ik}$,记$D_{ik}=D_i \cap C_k$,$|D_{ik}|$为$D_{ik}$的样本个数。
ID3算法如下
- 输入: 训练数据集$D$,特征集$A$,阈值$\epsilon$
- 输出: 决策树$T$
- 若$D$中所有实例属于同一类别$C_k$,则$T$为单结点树,并将类$C_k$作为该结点的类标记,返回$T$;
- 若$A=\emptyset$,则$T$为单点树,将$D$中实例数最多的类$C_k$作为该结点的类标记,返回$T$;
否则,如下计算$A$中各特征对$D$的信息增益,选择信息增益最大的特征$A_g$
- 计算数据集$D$的经验熵
$$H(D)=-\sum_{k=1}^{K}\frac{|C_k|}{|D|}log_2\frac{|C_k|}{|D|}$$ - 计算特征集$A$对数据集$D$的经验条件熵
$$H(D|A)=\sum_{i=1}^{n}\frac{|D_i|}{|D|}H(D_i)=\sum_{i=1}^{n}[\frac{|D_i|}{|D|}\sum_{k=1}^{K}\frac{|D_{ik}|}{|D_{i}|}log_2\frac{|D_{ik}|}{|D_{i}|}]$$ - 计算信息增益
$$g(D,A)=H(D) - H(D|A)$$
- 计算数据集$D$的经验熵
如果$A_g$小于阈值$\epsilon$,则置$T$为单点树,将$D$中实例数最多的类$C_k$作为该结点的类标记,返回$T$;
- 否则,对$A_g$的每一个值$a_i$,按照$A_g=a_i$将$D$分割为若干非空子集$D_i$,将$D_i$中实例最大的类作为标记,构建子结点,由结点和子结点构成树$T$,返回$T$
- 对第$i$个子结点,以$D_i$为训练集,以$A_i-{A_g}$为特征集,递归地调用步骤1-5,得到子树$T_i$,返回$T_i$
C4.5算法
C4.5算法和ID3算法类似,C4.5算法对ID3算法进行了改进,在生成模型的过程中采用信息增益比来选择特征。
示例
以贷款申请数据为例讲解决策树的生成过程,采用ID3算法。
| ID | 年龄 | 有工作 | 有自己的房子 | 信贷情况 | 类别 |
|---|---|---|---|---|---|
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
- 计算经验熵$H(D)$
$$H(D)=-\frac{6}{15}log_2\frac{6}{15}-\frac{9}{15}log_2\frac{9}{15}=0.971$$ 计算各特征对数据集$D$的信息增益
- 年龄
$$
\begin{split}
g(D,A_1)&=H(D) - [\frac{5}{15}H(D_1)+\frac{5}{15}H(D_2)+\frac{5}{15}H(D_3)]\\
&= 0.971 - {\frac{5}{15}[-\frac{2}{5}log_2\frac{2}{5}-\frac{3}{5}log_2\frac{3}{5}]+
\frac{5}{15}[-\frac{3}{5}log_2\frac{3}{5}-\frac{2}{5}log_2\frac{2}{5}]+
\frac{5}{15}[-\frac{4}{5}log_2\frac{4}{5}-\frac{1}{5}log_2\frac{1}{5}]}\\
&=0.971-0.888\\
&=0.083
\end{split}
$$ - 有工作
$$
\begin{split}
g(D,A_2)&=H(D) - [\frac{5}{15}H(D_1)+\frac{10}{15}H(D_2)]\\
&= 0.971 - {\frac{5}{15} \times 0+
\frac{10}{15}[-\frac{6}{10}log_2\frac{6}{10}-\frac{4}{10}log_2\frac{4}{10}]}\\
&=0.971-0.647\\
&=0.324
\end{split}
$$ - 有自己的房子
$$
\begin{split}
g(D,A_3)&=H(D) - [\frac{6}{15}H(D_1)+\frac{9}{15}H(D_2)]\\
&= 0.971 - {\frac{6}{15} \times 0+
\frac{9}{15}[-\frac{3}{9}log_2\frac{3}{9}-\frac{6}{9}log_2\frac{6}{9}]}\\
&=0.971-0.551\\
&=0.420
\end{split}
$$ - 信贷情况
$$
\begin{split}
g(D,A_3)&=H(D) - [\frac{5}{15}H(D_1)+\frac{6}{15}H(D_2)+\frac{4}{15}H(D_2)]\\
&= 0.971 - {\frac{5}{15}[-\frac{1}{5}log_2\frac{1}{5}-\frac{4}{5}log_2\frac{4}{5}] +
\frac{6}{15}[-\frac{4}{6}log_2\frac{4}{6}-\frac{2}{6}log_2\frac{2}{6}] +
\frac{4}{15} \times 0 }\\
&=0.971-0.608\\
&=0.363
\end{split}
$$
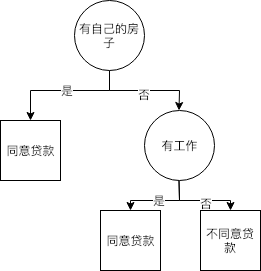
综上,特征$A_3$(有自己的房子)的信息增益值最大,所以选择$A_3$作为根节点的特征。接下来将数据集$D$划分为两个子集$D_1$($A_3$=是)、$D_2$($A_3$=否),分别进行下一轮的信息增益筛选。
- 年龄
- 进入子集$D_1$($A_3$=是),由于该子集中只有一个类别,所以形成叶子结点,结点的标记就是类别。
进入子集$D_2$($A_3$=否),数据如下
计算经验熵
$$H(D_2)=-\frac{6}{9}log_2\frac{6}{9}-\frac{3}{9}log_2\frac{3}{9}=0.918$$年龄特征信息增益
$$
\begin{split}
g(D_2,A_1)&=H(D) - [\frac{4}{9}H(D_1)+\frac{2}{9}H(D_2)+\frac{3}{9}H(D_3)]\\
&= 0.971 - {\frac{4}{9}[-\frac{3}{4}log_2\frac{3}{4}-\frac{1}{4}log_2\frac{1}{4}]+
\frac{2}{9}\times0+
\frac{3}{9}[-\frac{2}{3}log_2\frac{2}{3}-\frac{1}{3}log_2\frac{1}{3}]}\\
&=0.971-0.667\\
&=0.251
\end{split}
$$有工作特征信息增益
$$
\begin{split}
g(D_2,A_2)&=H(D) - [\frac{6}{9}H(D_1)+\frac{3}{9}H(D_2)]\\
&= 0.971 - [\frac{6}{9}\times0+\frac{3}{9} \times 0]\\
&= 0.918-0\\
&=0.918
\end{split}
$$信贷情况特征信息增益
$$
\begin{split}
g(D_2,A_4)&=H(D) - [\frac{4}{9}H(D_1)+\frac{4}{9}H(D_2)+\frac{1}{9}H(D_3)]\\
&= 0.971 - {\frac{4}{9}\times0+
\frac{4}{9}[-\frac{2}{4}log_2\frac{2}{4}-\frac{2}{4}log_2\frac{2}{4}]+
\frac{1}{9}\times0}\\
&=0.918-0.444\\
&=0.474
\end{split}
$$
综上,特征$A_2$(有工作)的信息增益值最大,所以选择$A_2$作为该结点的特征。接下来将数据集$D_2$划分为两个子集$D_{21}$($A_2$=是)、$D_{22}$($A_2$=否),分别进行下一轮的信息增益筛选。
进入子集$D_{21}$($A_2$=是),由于该子集中只有一个类别,所以形成叶子结点,结点的标记就是类别
- 进入子集$D_{22}$($A_2$=否),由于该子集中只有一个类别,所以形成叶子结点,结点的标记就是类别
最终产生的决策树模型如下图所示
代码
1 |
|
参考
- 机器学习实战,人民邮电出版社
- 统计学习方法,清华大学出版社