机器学习主要解决两类问题：回归和分类，上篇文章中的线性回归模型是回归模型的一种，但并不能用于分类问题，本文将介绍一种可以用于分类问题的回归算法–logistic回归。

利用logistic回归进行分类的主要思想是：估算某个实例属于特定类别的概率，如果预估概率超过50%，则属于该类别；反之，属于其他类别，这样形成了一个简单的二元分类器。

原理

sigmoid函数

我们希望能找到一种根据输入值输出0，1分类的函数，脑海中闪现的第一个函数应该就是单位阶跃函数，即
$$
\delta(x)=
\begin{cases}
0, & x \leq 0; \\
1, & x>0.
\end{cases}
$$
但是该函数在$x=0$处不可导，对于公式推导来说有很大问题，所以大牛们找到了sigmoid函数来代替阶跃函数。

Sigmoid函数公式如下

$$
f(x)=\frac{1}{1+e^{-x}}
\tag{1}
$$

其函数图像如下所示

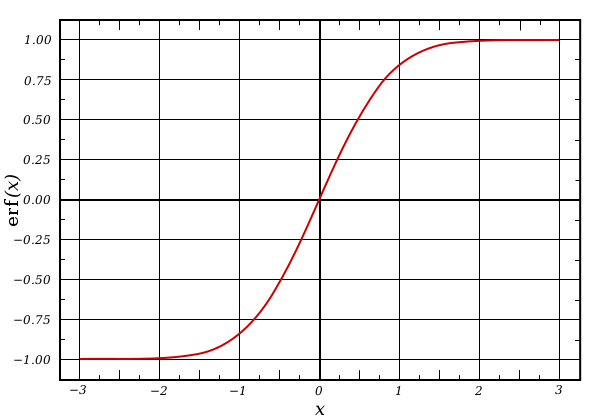
logistic回归模型

将公式1推广到多维场景：给每个特征都乘以一个回归系数并相加，即$z=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+……+\theta_{n}x_{n}=\theta ^{T}x$（线性回归），然后将总和带入sigmoid函数中得到
$$
h_{\theta}\left(x \right)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta ^{T}x}}
\tag{2}
$$
所以线性回归的的结果被映射到了sigmoid函数中。在sigmoid函数图像中可以看出，其函数值介于0～1，中间值为0.5，因此$h_{\theta}\left(x \right)$的输出可以看作分类的概率。当$h_{\theta}\left(x \right)>0.5$，说明$x$属于A类；反之，$h_{\theta}\left(x \right)<0.5$，则$x$属于B类。

参数估计

对于给定的数据集$T={(x_1,y_1),(x_2,y_2),…(x_n,y_n)}$，其中$x_i \in R^n$，$y_i \in {0,1}$。分类结果为1的概率表示为
$$
P(y=1|x;\theta)=h_\theta(x)
$$
分类结果为0的概率表示为
$$
P(y=0|x;\theta)=1-h_\theta(x)
$$
将其合并则有
$$
p(y|x;\theta)=h_\theta(x_i) ^{y_i}(1-h_\theta(x))^{1-y_i}
$$
因为m个样本互相独立，所以其联合分布可以看作各个样本概率之积，则似然函数为
$$
L(\theta) = \prod_{i=1}^{n}p(y_i|x_i;\theta)=\prod_{i=1}^{n} [h_\theta(x_i)]^{y_i}[1-h_\theta(x_i)]^{1-y_i}
$$
取对数似然
$$
l(\theta) =\sum_{i=1}^{n} y_ilog[h_\theta(x_i)]+(1-y_i)log[1-h_\theta(x)]
\tag{3}
$$
当$l\left(\theta \right)$取最大值时，$\theta$的值为最终的解。求$l\left(\theta \right)$对$\theta$的导数

$$
\begin{split}
l^{‘}(\theta)&=\sum_{i=1}^{n} [\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)}] \cdot h^{‘}_\theta(x_i)\\
&=\sum_{i=1}^{n} [\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)}]\cdot[h_\theta(x_i)]^{‘}_{z} \cdot z^{‘}_\theta\\
&=\sum_{i=1}^{n}[\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)}] \cdot h_\theta(x_i)[1-h_\theta(x_i)] \cdot z^{‘}_\theta \\
&=\sum_{i=1}^{n}[y_i-h_\theta(x_i)] \cdot x_i
\end{split}
\tag{4}
$$

* 注：sigmoid求导结果
$$
f’\left(x \right)=f\left(x \right)\left[1-f\left(x \right) \right]
$$

<\font>
对公式4进行迭代，可求得参数$\theta$。

思考

对偏置项b的处理

在大部分资料中，会在输入$x$和权重$\theta$中增加一列常数列作为偏置项，这样做的好处是不需要对其进行单独处理，可随权重$\theta$一起求解，下面来讨论一下单独求解偏置项$b$的步骤。

假设输入为$[x_1,x_2,…,x_n]$，权重为$[\theta_1,\theta_2,…,\theta_n]$，偏置项为$[b_1,b_2,…,b_n]$，则公式2变为
$$
h_{\theta}\left(x \right)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta ^{T}x-b}}
$$
接下来需让公示3对变量b求导
$$
\begin{split}
l^{‘}(b)&=\sum_{i=1}^{n} [\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)}] \cdot h^{‘}_\theta(x_i)\\
&=\sum_{i=1}^{n} [\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)}] \cdot [h_\theta(x_i)]^{‘}_{z} \cdot z^{‘}_b\\
&=\sum_{i=1}^{n}[\frac{y_i}{h_\theta(x_i)}-\frac{1-y_i}{1-h_\theta(x_i)}] \cdot h_\theta(x_i)[1-h_\theta(x_i)] \cdot z^{‘}_b \\
&=\sum_{i=1}^{n}[y_i-h_\theta(x_i)] \cdot x_i
\end{split}
\tag{5}
$$
对公式5进行迭代，可求得参数$b$。

代码实现

为了加深对公示的理解，代码没有直接使用tensorflow内置的优化器，手动实现了逻辑回归梯度下降。示例如下：


# coding=utf-8
import tensorflow as tf
from sklearn import datasets
import numpy as np
from sklearn.preprocessing import OneHotEncoder

iris = datasets.load_iris()
data_x = np.array(iris['data'])
data_y = np.array(iris['target']).reshape(-1, 1)
print data_x.shape
print data_y.shape
enc = OneHotEncoder()
enc.fit(data_y)
# 多分类问题，对label进行one-hot编码
targets = enc.transform(data_y).toarray()
# 输入行数不指定，列数为特征个数
X = tf.placeholder(dtype=tf.float32, shape=(None, data_x.shape[1]))
# 输出行数不指定，列数类别个数
y = tf.placeholder(dtype=tf.float32, shape=(None, 3))
# 学习率
alpha = 0.0001
# 迭代次数
epoch = 500
# 权重
theta = tf.Variable(tf.random_uniform([data_x.shape[1], 3], -1.0, 1.0), name='theta')
# 偏置
b = tf.Variable(tf.random_uniform([3], -1.0, 1.0), name='b')
# 预测值
predict_y = tf.nn.softmax(tf.matmul(X, theta) + b)
# 误差
error = tf.cast(y, tf.float32) - predict_y
# 代价函数，使用交叉熵函数，手动实现
cost = tf.reduce_mean(-tf.reduce_sum(y * tf.log(predict_y), reduction_indices=1))
# 权重的负梯度
theta_gradient = -tf.matmul(tf.matrix_transpose(X), error, name='theta_gradient')
# 偏置的负梯度
b_gradient = - tf.reduce_mean(tf.matmul(tf.transpose(X), error), reduction_indices=0, name='b_gradient')
# 权重迭代项
training_op1 = tf.assign(theta, theta - alpha * theta_gradient)
# 偏置迭代项
training_op2 = tf.assign(b, b - alpha * b_gradient)
# 全局初始化
init = tf.global_variables_initializer()
with tf.Session() as sess:
    init.run()
    for i in range(epoch):
        sess.run([training_op1, training_op2, cost], feed_dict={X: data_x, y: targets})
        print sess.run(theta, feed_dict={X: data_x, y: targets})
        print sess.run(b, feed_dict={X: data_x, y: targets})
        print sess.run(cost, feed_dict={X: data_x, y: targets})

代码详见逻辑回归代码

参考

Tensorflow实现梯度下降各种方法
机器学习实战-基于Scikit-Learn和Tensorflow，机械工业出版社
机器学习实战，人民邮电出版社