上一篇博客介绍了knn算法,以及简单的python实现代码,其中使用了线形扫描(linear scan)方式逐一计算输入实例与训练数据间的距离,复杂度较大,本篇博客将介绍knn算法的另一种高效实现方式–kd树。
简介
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树,表示对k维空间的一个划分。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分,构成一系列的k维超矩形区域。kd树每个节点对应一个k维超矩形区域。在进行k近邻查找时,遍历kd树,实现减少计算量的目的。
原理
构建kd树
定义节点
- 算法描述
首先需要定义二叉树节点Node,其中需要包括的信息有
| 域名 | 数据类型 | 描述 |
|---|---|---|
| point | 数据矢量 | 数据集中的一个数据点,是一个k维矢量 |
| split | 正整数 | 分割维度 |
| left | kd树 | 左子树 |
| right | kd树 | 右子树 |
| label | 字母或数字 | 标签值 |
- python实现
1 | #encoding:utf8 |
构建平衡kd树
算法描述
输入:K维空间数据集$T=\lbrace x_1,x_2,…,x_n\rbrace$,其中$x_i = (x_i^{(1)},x_i^{(2)},…,x_i^{(k)})^T$,$i=1,2,…,N$
输出:kd树
过程:
- 构造根节点,根据点对应于包含T的k维空间的超矩形区域
- 选择方差最大的维度$m$为分割维度,以T中所有实例的$x^m$坐标中位数N为切分点,将根节点的超矩形区域分割为深度为1的两个左右子节点。左子节点对应坐标$x^m$小于N的子区域,右子节点对应于坐标$x^m$大于N的子区域。将切分点保存在根节点。
- 在左右子区域上分别重复执行步骤2,直到两个子区域没有实例存在时停止,完成kd树的构建
python实现
1 | #encoding:utf8 |
搜索kd树
kd树相当于给训练数据建立了索引,所以利用kd树可以快速搜索到距离输入实例最近的训练数据点。
算法描述
- 输入:构造好的kd树,输入实例x
- 输出:x的最近邻
- 过程:
- 在kd树中搜索包含输入实例x的叶子结点:从根节点向下递归访问kd树,若输入实例当前维度的坐标小于切分点坐标,则移动到左子树;否则,则移动到右子树。直到子节点为叶子结点为止。
- 以叶子结点为“当前最近结点”
- 递归回溯,在每个节点上进行下列操作:
- 如果该节点保存的实例点比当前最近距离目标更近,则以该实例点为“当前最近结点”
- 检查其子节点对应的区域是否有更近的点,即检查子节点对应的区域是否与以目标点为中心、以”当前最近距离”为半径形成的超球体相交。如果相交,则在对应的区域内可能存在距目标点更近的点,则移动到该结点,递归地进行搜索。若不相交,则向上回退。
- 当回退到根节点,搜索结束,最后的“当前结点“即为x的最近邻。
python实现
1 | def find_nearest_neighbor(target,tree): |
代码详见kdtree
示例
以《统计学习方法》中的例题为例,直观地解释kd树的构建和搜索。
问题描述
给定一个二维空间的数据集$T=\lbrace(2,3)^T,(5,4)^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T\rbrace$,其在二维空间中的位置如图所示,求点(2.1,3.1)和(2,4.5)的最近邻。
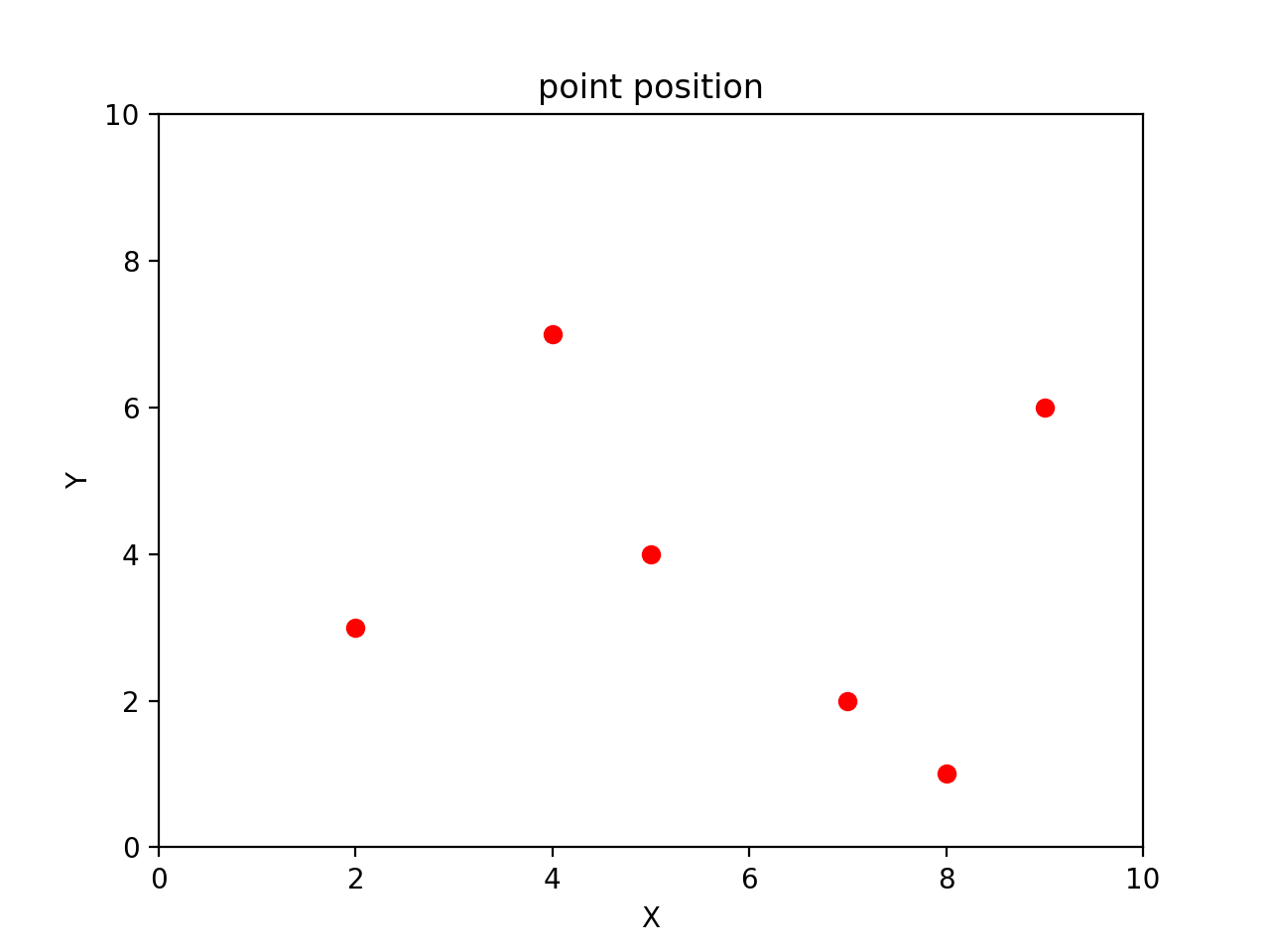
构建kd树
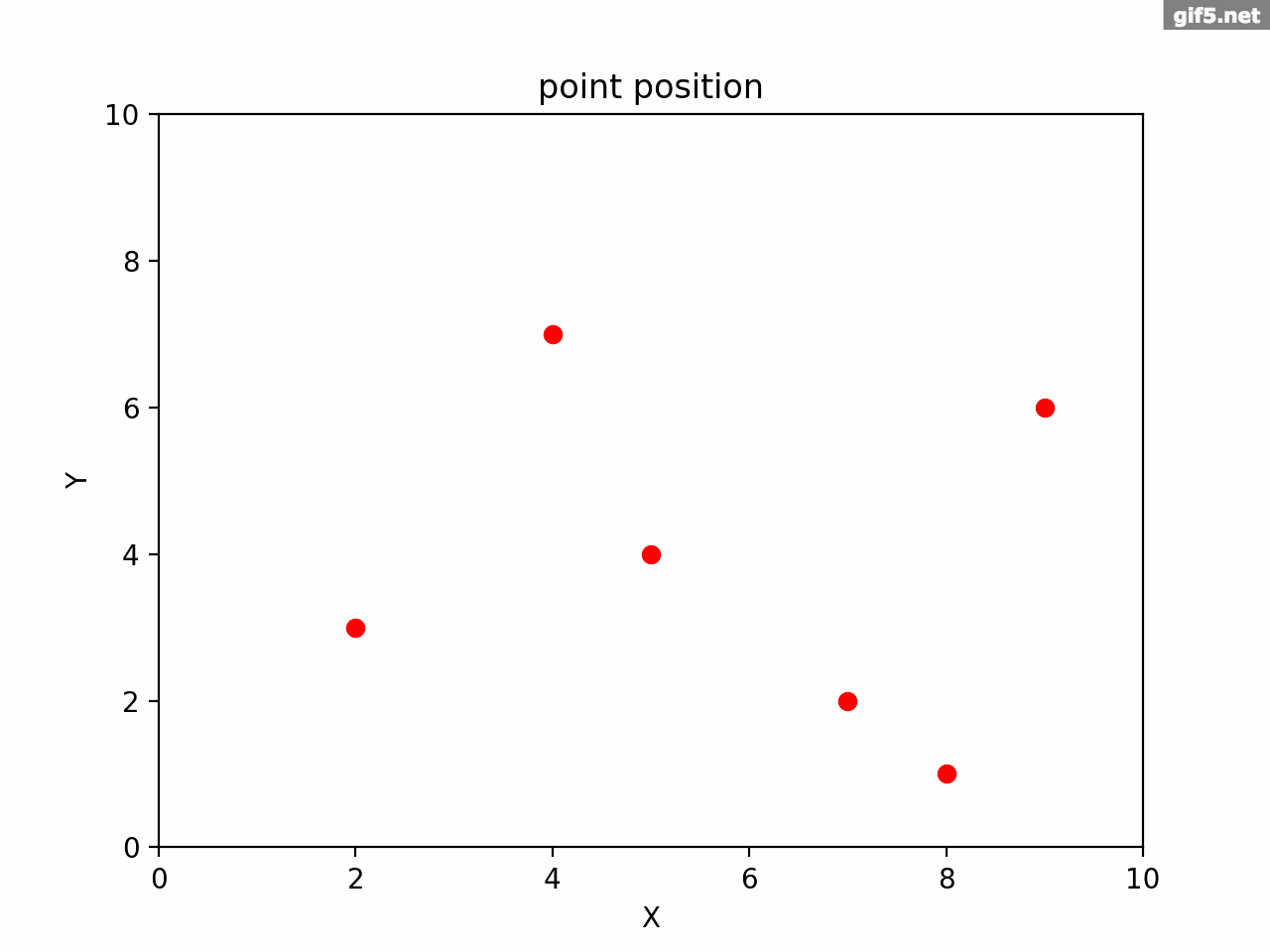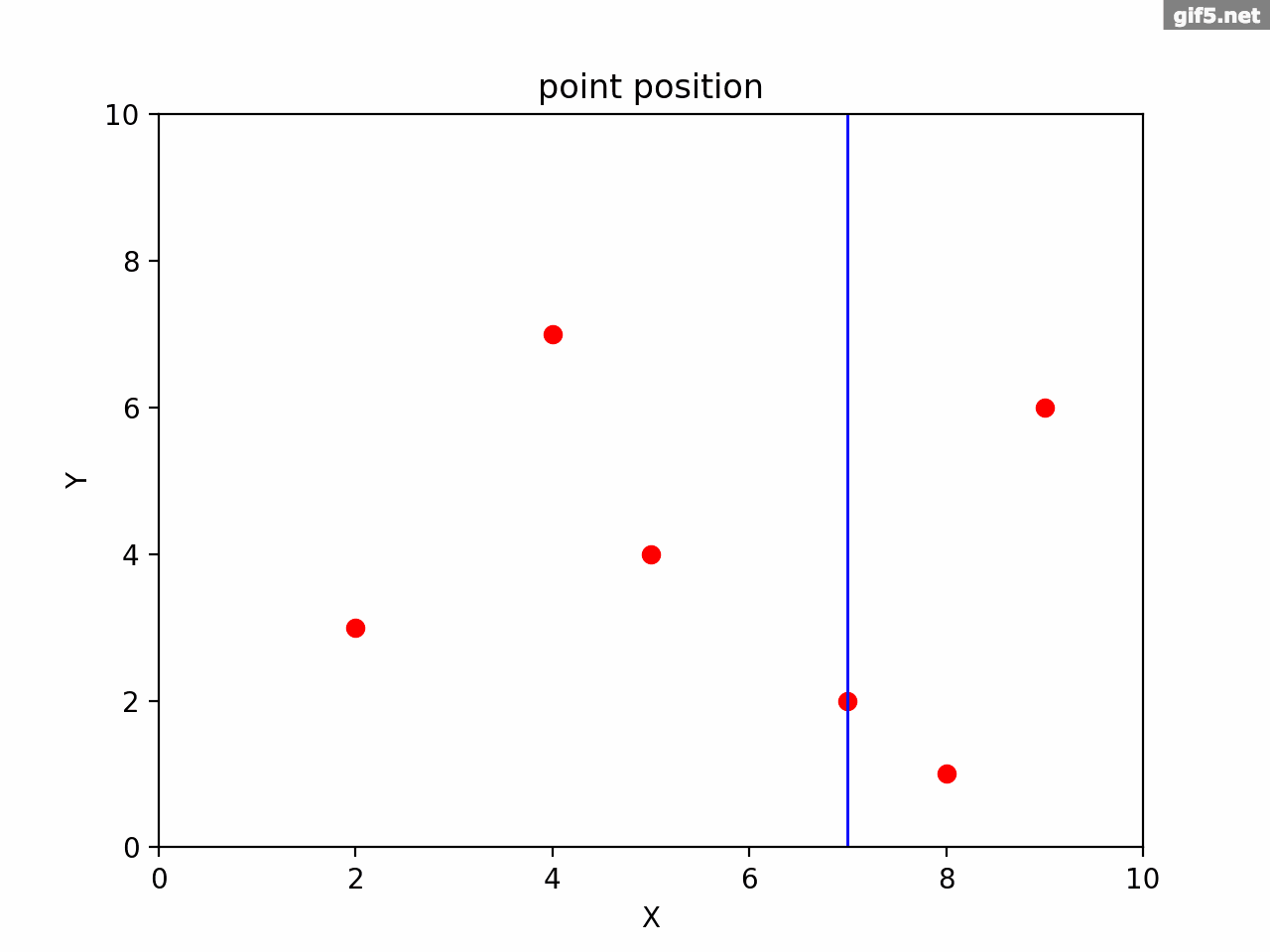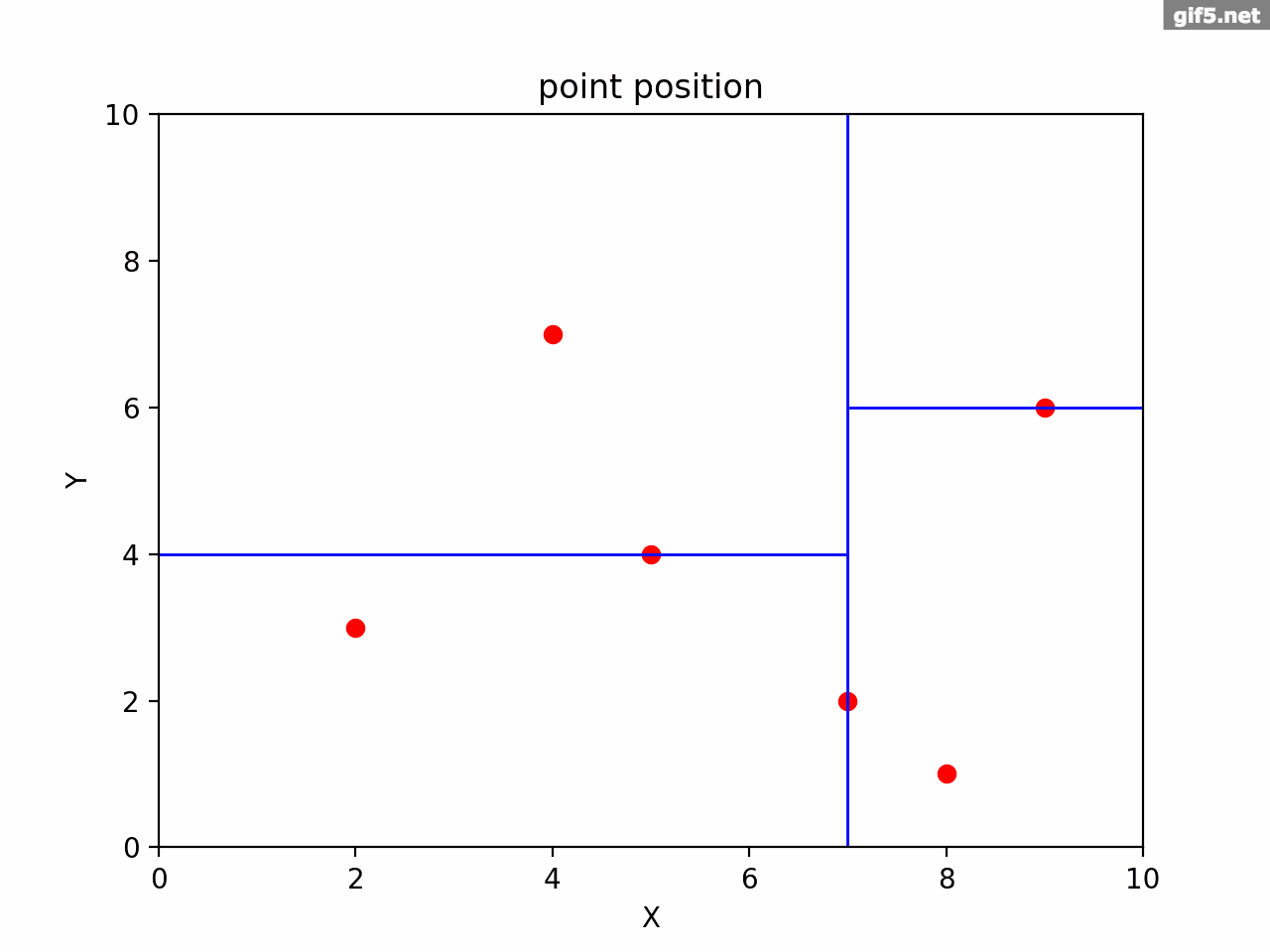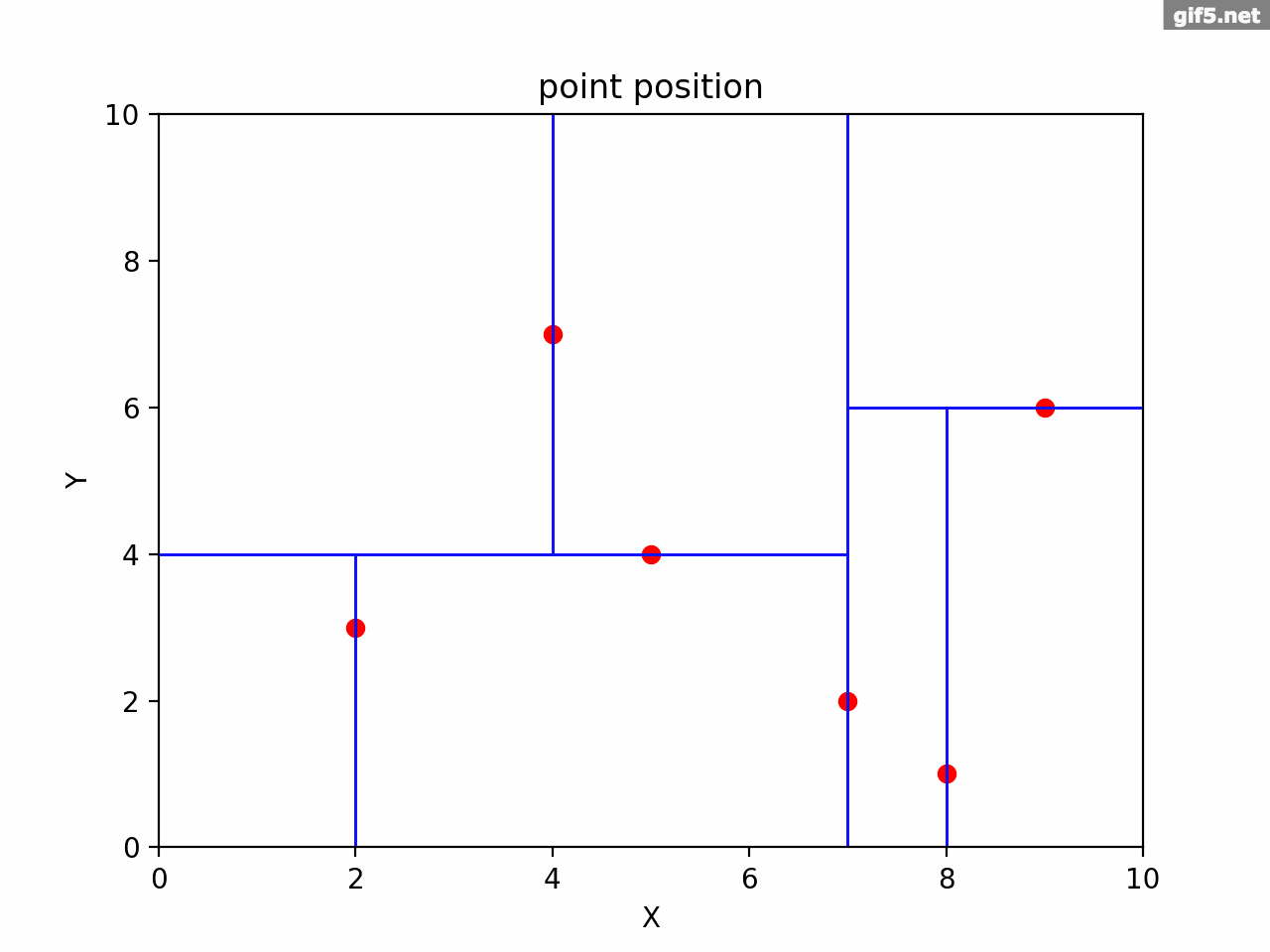
首先,计算x、y方向上的方差,其中var(x)=5.805,var(y)=4.472,x方向上的方差更大所以先选取x方向为分割方向。
其次,选择x方向上的中位数,即(4,7)^T,空间划分如下图
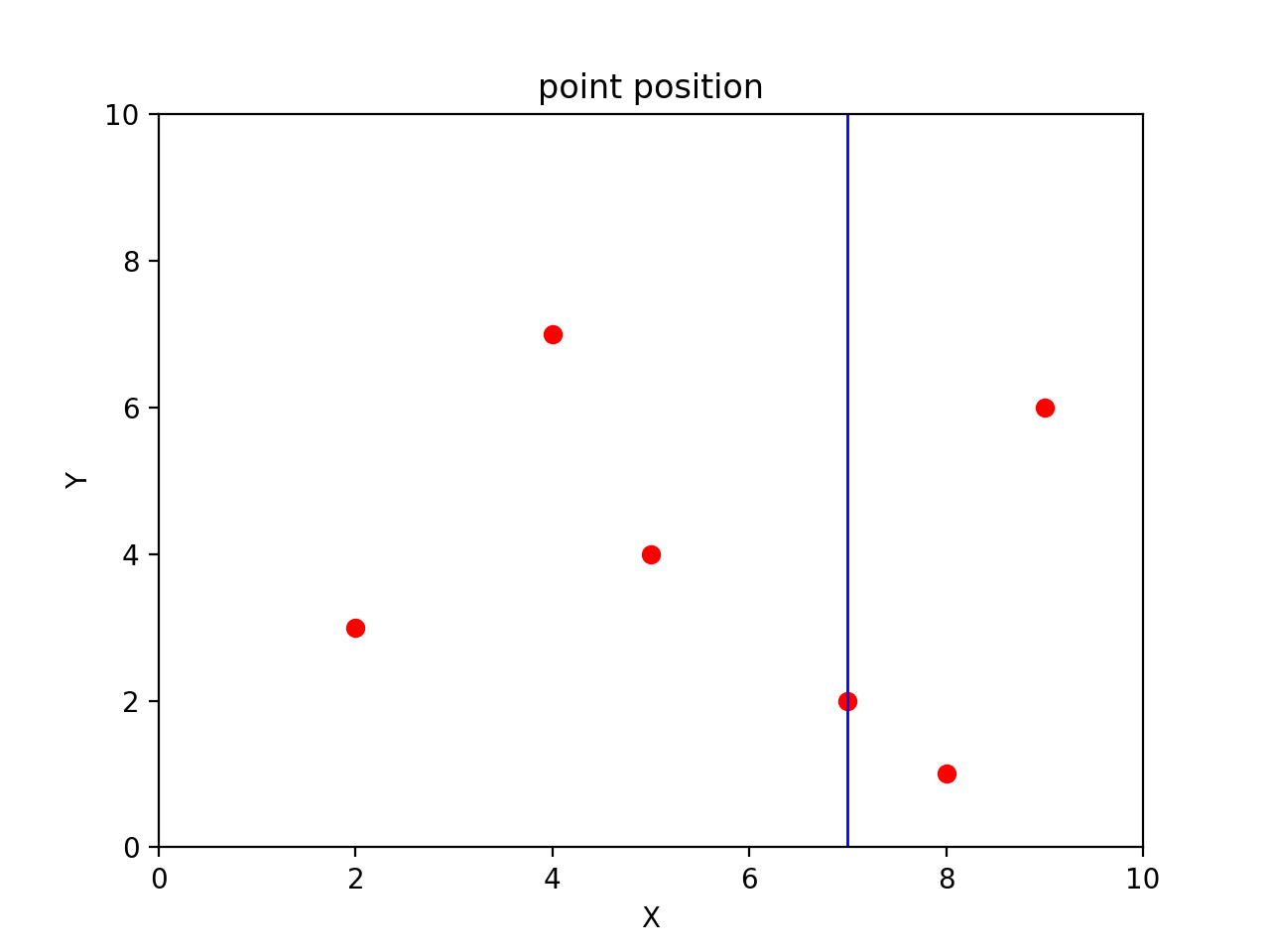
以此类推,经过三次划分构建好kd树,如gif所示
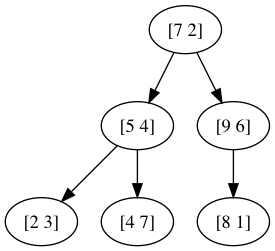
构建的树形结构如下图所示
搜索kd树
点(2.1,3.1)的最近邻
首先在kd树上搜索距离点(2.1,3.1)最近的叶子结点,结果为(2,3),距离为0.1414,搜索过程如下所示
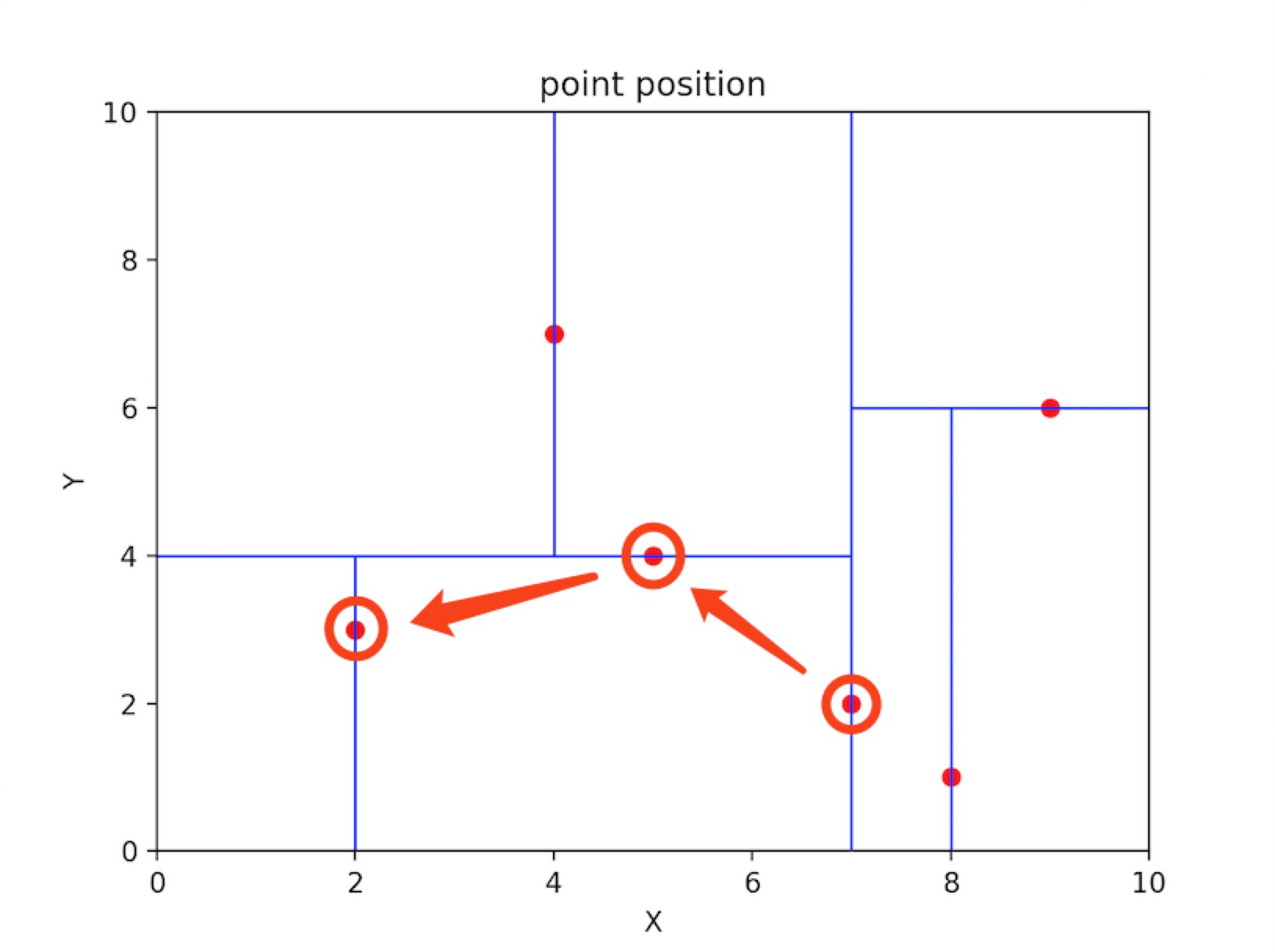
但是叶子结点不一定是离点(2.1,3.1)最近的结点,所以向上进行回溯。先回溯到父节点(5,4),计算距离为3.036,不满足最近邻要求。接下来判断是否需要进入父节点的其他子节点空间,以(2.1,3.1)为圆心,0.1414为半径画圆,发现该圆与切分超平面y=4不相交,因此不进入(5,4)右子节点搜索。
继续向上回溯到父节点(7,2),计算距离为5.022,不满足最近邻要求。接下来判断是否需要进入父节点的其他子节点空间,以(2.1,3.1)为圆心,0.1414为半径画圆,如下图所示发现该圆与切分超平面x=7不相交,因此不进入(7,2)右子节点搜索。
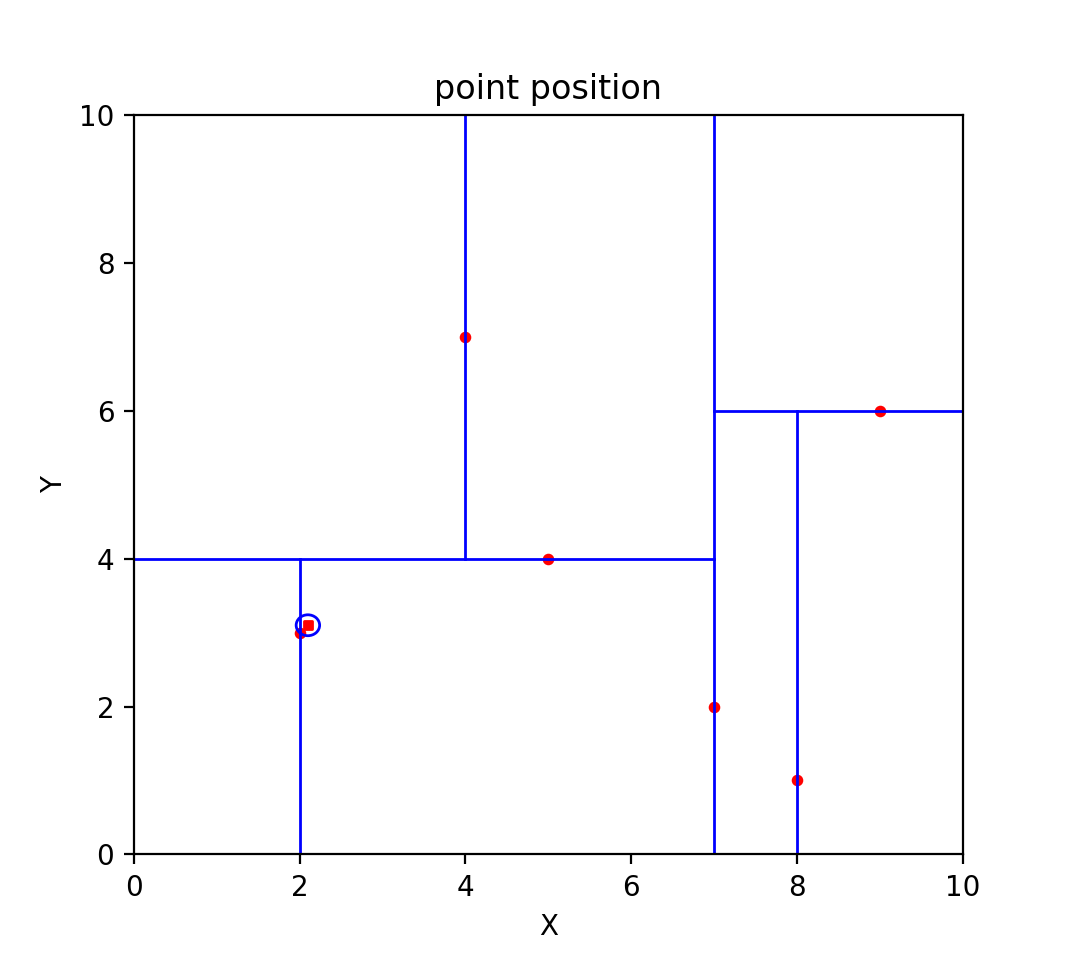
至此,搜索路径中的结点已经完全回溯完,返回最近邻节点(2,3),距离为0.1414。
点(2,4.5)的最近邻
同理先搜索叶子结点,过程如下所示
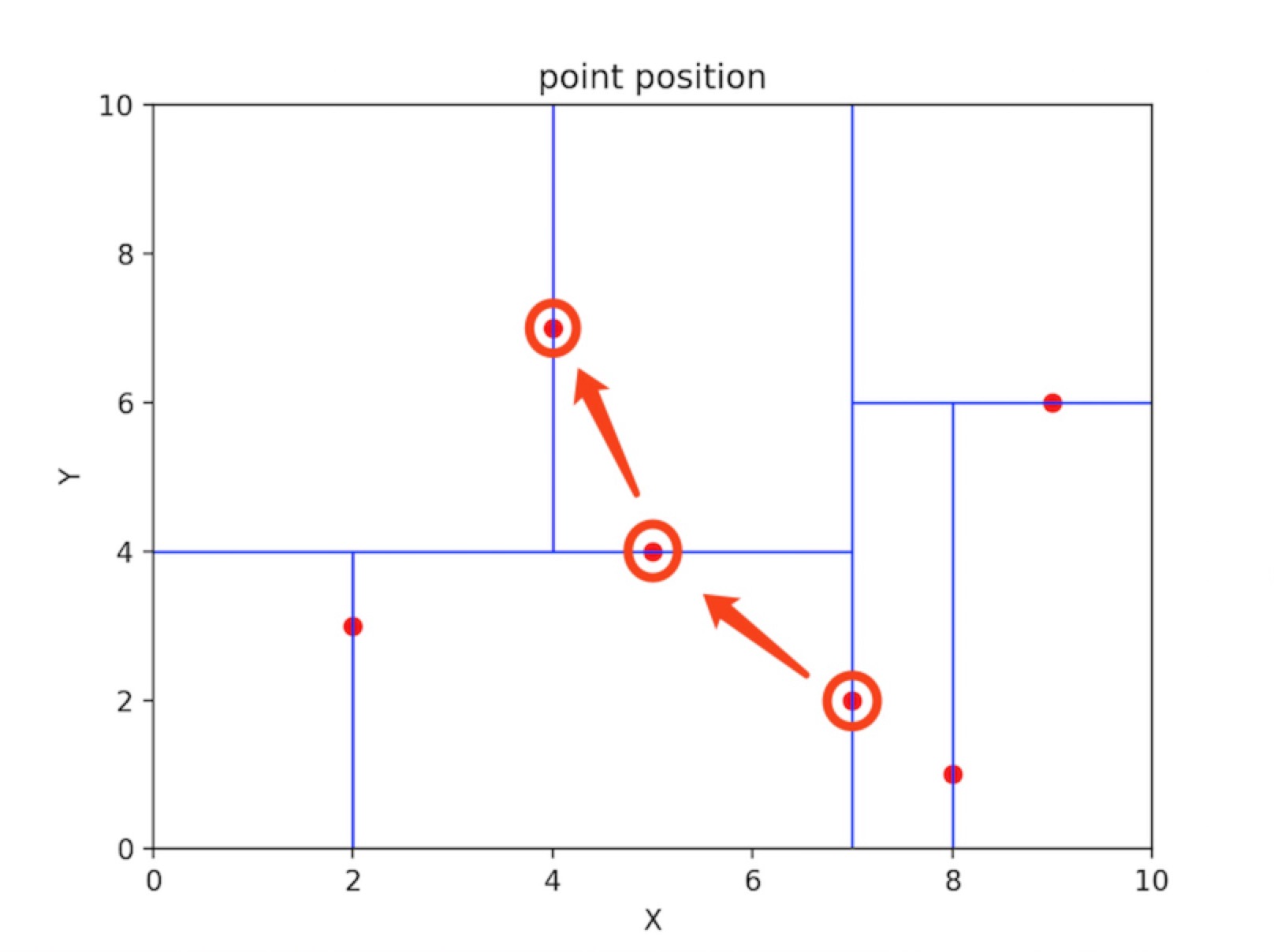
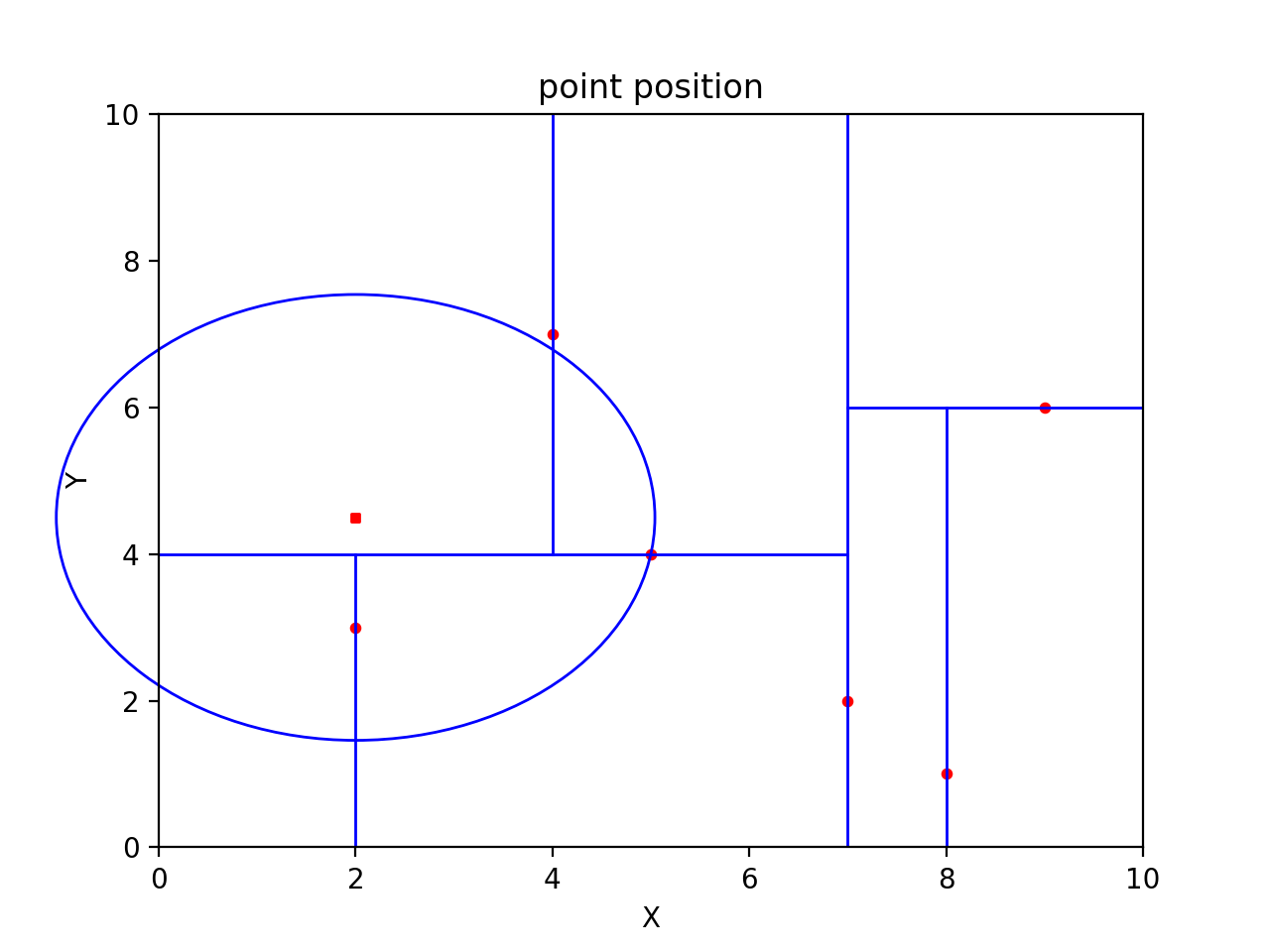
叶子结点为(4,7),距离为3.202。回溯到父节点(5,4),计算距离为3.041,最近邻更新为该点。接下来判断是否需要进入父节点的其他子节点空间,以(2,4.5)为圆心,3.041为半径画圆,如下图所示,发现该圆与切分超平面y=4相交,因此进入(5,4)左子节点搜索。
计算与点(2,3)距离为1.5,最近邻更新为当前节点。
继续向上回溯到父节点(7,2),计算距离为5.59,不满足最近邻要求。接下来判断是否需要进入父节点的其他子节点空间,以(2,4.5)为圆心,1.5为半径画圆,发现该圆与切分超平面x=7不相交,因此不进入(7,2)右子节点搜索。
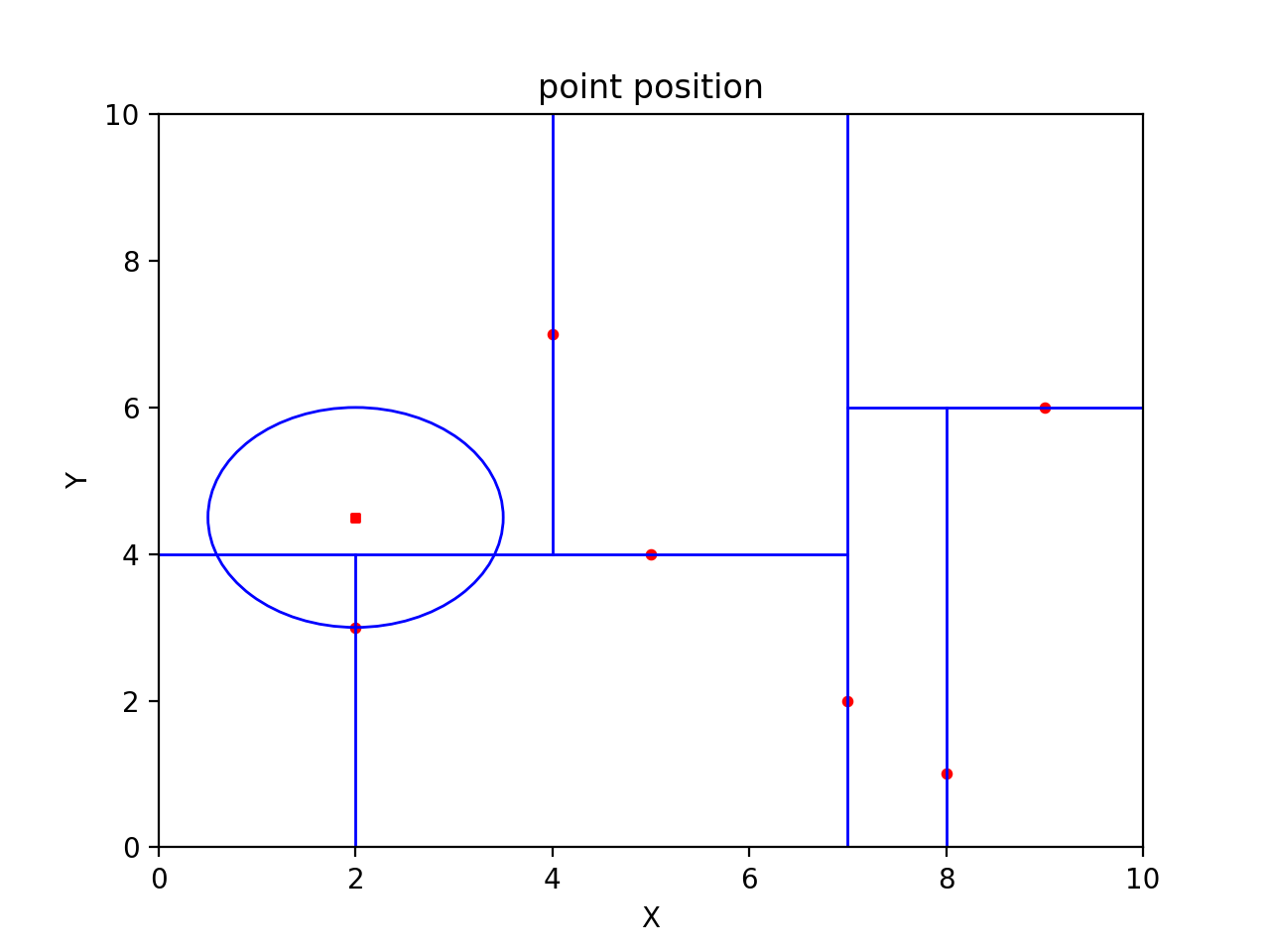
至此,搜索路径中的结点已经完全回溯完,返回最近邻节点(2,3),距离为1.5。
参考
统计学习方法,李航,清华大学出版社
机器学习实战,Peter Harrington,人民邮电出版社