课程01《神经网络和深度学习》的学习告一段落,这周开始课程02《改善深层神经网络:超参数调试、正则化及优化》的学习,第一周课程讲述了数据集的划分、方差与偏差的概念、正则化、梯度消失和梯度爆炸等知识点,都是在实际应用中会遇到的一些问题。
数据集的划分
首先明确一下训练集、验证集和测试集的概念,之前很少强调验证集,导致把验证集和测试集的概念混淆。
训练集
训练集(training set)用来构建模型、确定模型参数的样本。
验证集
验证集(validation set)用于模型优化、确定网络结构或者控制模型复杂程度的参数,主要是辅助模型构建。
测试集
测试集(training set)用于检验训练好的模型的预测能力。
以前没有仔细区分验证集和测试集,一些demo也只是将数据集划分为training set和test test,此处需要注意验证集的基本概念。ng在视频中说对一般量级的数据进行划分的时候,可以取训练集:验证集:测试集=3:1:1的比例;如果分为两类,一般是训练集:测试集=7:3。在大数量级数据的情况下,验证集和测试集占的比例可能较小。ng特意强调了保证测试集和验证集来自同一分布
方差与偏差
方差
方差描述的是预测值相对于期望值的波动范围,也可以说是离散程度。方差越大,数据的分布越分散,波动范围越大;反之亦然。
偏差
描述的是预测值的期望与真实值之间的差距。偏差越大,和真实值差的越多。
下图比较形象的说明了两者的区别
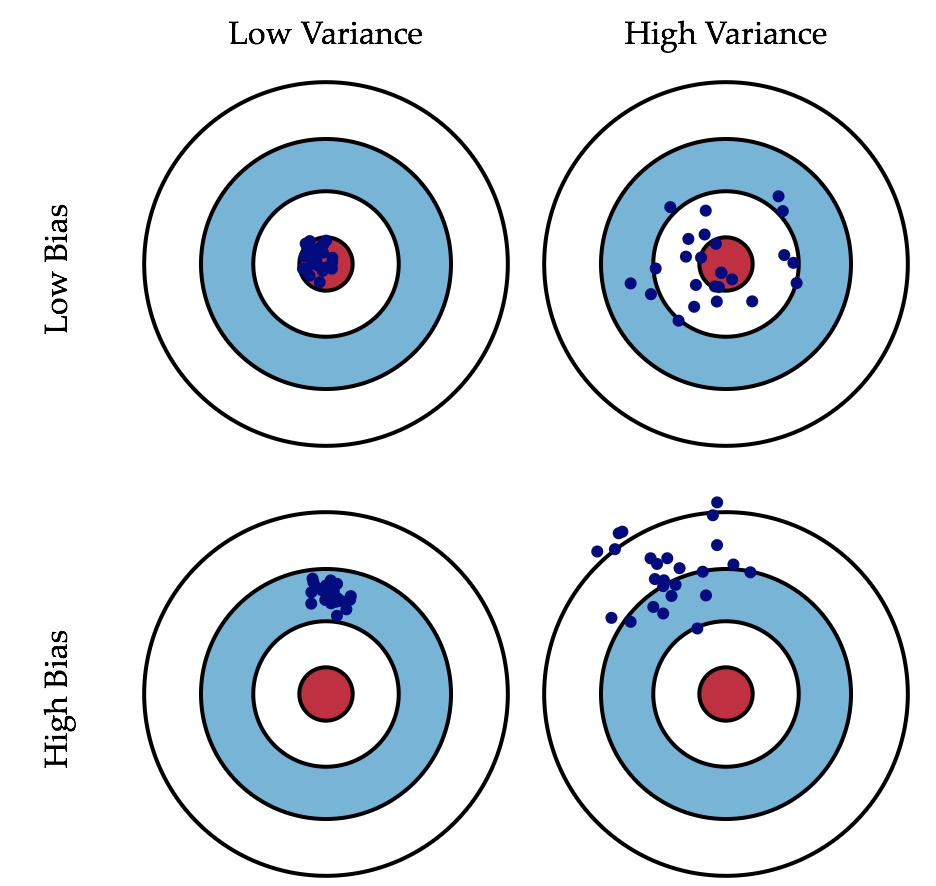
正则化
当模型在训练集的效果在训练集上效果表现很好,但是在测试集上表现很差的话,说明出现了过拟合的情况。举个例子来说,就好比上学的时候做练习题,如果一个学生练习题做的很好,但是考试好不过,说明学习方法有问题,不能很好的掌握所学知识,出现了过拟合的问题。解决过拟合的问题有以下几种方法:数据集扩增、early stopping、正则化。
数据集扩增
对抗过拟合的一个有效方法就是用更多的训练数据去训练模型,用于训练模型的数据多了,说明模型使用范围更广泛。就好比一个学生做的练习题多了,把知识都融会贯通了,考试自然就能考高分。
数据集扩增不太容易办到,ng讲了几个例子可以较方便的扩展数据集,主要包括产生镜像图片、旋转原图、图像加噪声等。
early stopping
随着代价函数的不断减小,训练误差是一个不断变小的过程,验证误差起初也会不断减小,但是当出现过拟合的时候验证误差会慢慢增加,eraly stopping就是在验证误差即将增大的时候停止迭代的过程。下图能比较明显的表示这个过程。
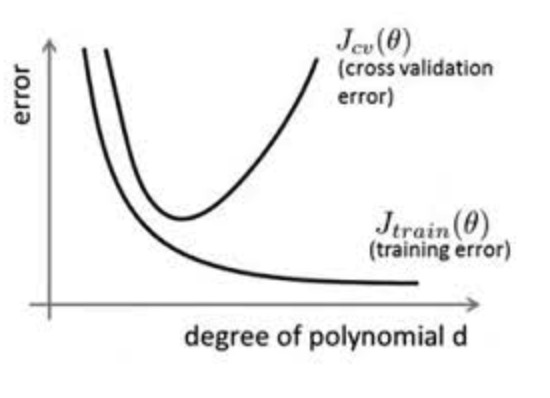
正则化
正则化方法是指在进行目标函数优化时,在目标函数后面加上一个正则项,来达到防止过拟合的目的,即$C = J(W,b)+R$,其中$J(W,b)$是原损失函数,$R$是正则项。常见的正则项有L1正则和L2正则。
L1正则化
L1正则化就是在原损失函数基础上加上L1范数,即$C = J(W,b)+\frac{\lambda}{n}\sum^{n}_{i=1}|w_{i}|$。L1正则化对所求权重产生的影响从下面推导的过程看出来,首先求导
$$\frac{\partial{C}}{\partial{w}}=\frac{\partial{J(W,b)}}{\partial{w}}+\frac{\lambda}{n}sign(w)$$
则梯度更新的过程为
$$w:=w-\eta\frac{\partial{J(W,b)}}{\partial{w}}-\eta\frac{\lambda}{n}sign(w)$$
当$w>0$时,更新后的$w$变小;而当$w<0$时,更新后的$w$变大,所以产生的效果就是使得$w$趋近于0。
L2正则化
L1正则化就是在原损失函数基础上加上L1范数,即$C = J(W,b)+\frac{\lambda}{2n}\sum^{n}_{i=1}w_{i}^2$。同样可以通过推导来看L2范数对权重产生的影响,首先求导
$$\frac{\partial{C}}{\partial{w}}=\frac{\partial{J(W,b)}}{\partial{w}}+\frac{\lambda}{n}w$$
则梯度更新的过程为
$$w:=w-\eta\frac{\partial{J(W,b)}}{\partial{w}}-\eta\frac{\lambda}{n}w = (1-\eta\frac{\lambda}{n})w-\eta\frac{\partial{J(W,b)}}{\partial{w}}$$
因为$\eta,\lambda,n$都是大于0的,所以更新后的$w$相对于没加L2正则的时候变小了,有缩减系数的效果。
DropOut正则化
Dropout是深度学习正则化的一种方式,它指按照一定的概率将一些神经元暂时从网络中丢弃,被丢弃的神经元不会对后面的计算产生影响,效果如下图。
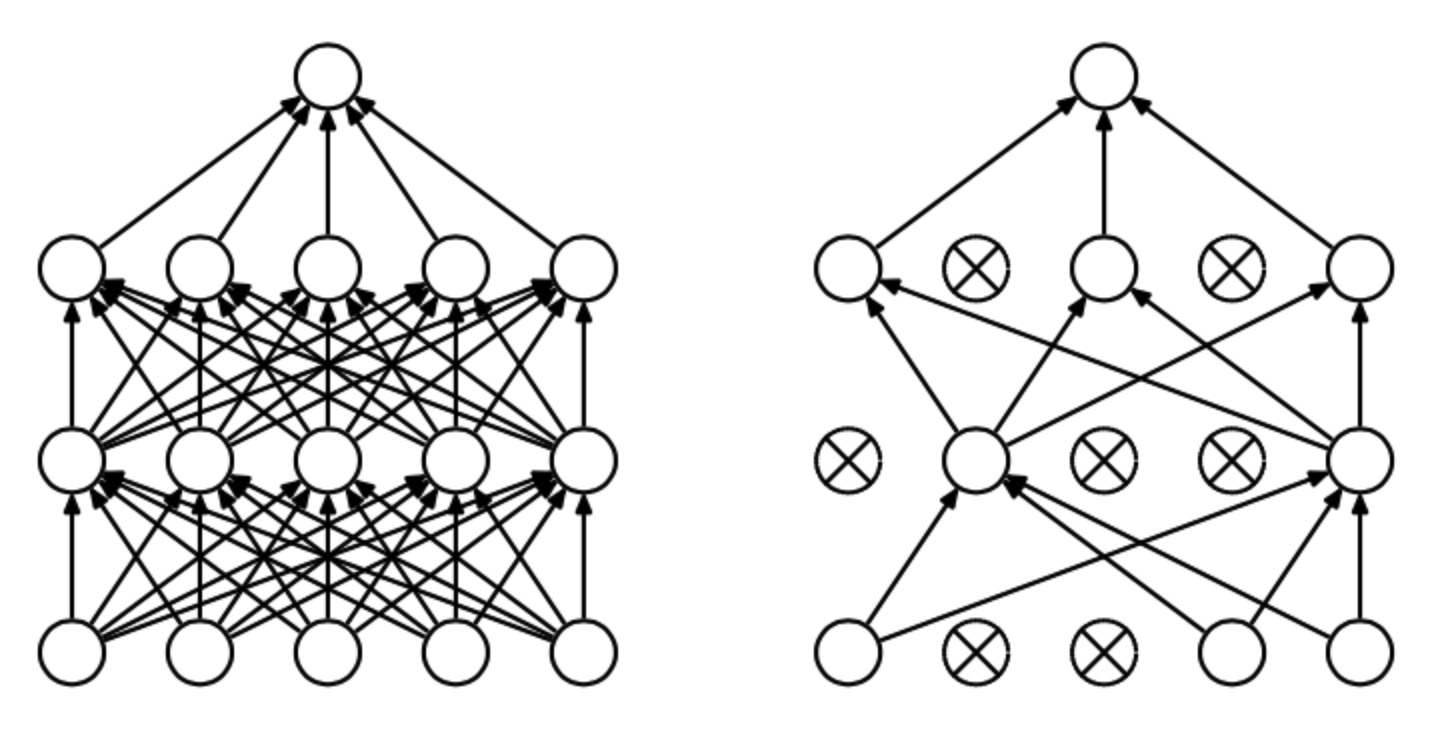
梯度消失和梯度爆炸
假设有n层网络,b暂时忽略不计,激活函数为线性激活函数,则一个神经元的输出为$z=Wx$,那么经过n层网络输出为
$$y=W^{(n)}W^{(n-1)}W^{(n-2)}……W^{(2)}W^{(1)}x$$
所以当$W$的值稍比单位矩阵大,经过指数变换,得到的结果会很大;相应的若$W$的值稍比1小,经过指数变换,得到的结果也会变小。
考虑激活函数的话也会产生类似的效果,所以在搭建神经网络时,要考虑激活函数和权重初值,避免出现梯度消失和梯度爆炸的情况。
小结
关于正则化的问题,有两点要说明。首先,对于正则化缩减系数的理解:所求的$w$是特征的权重值,当出现过拟合时,几乎样本中的每个点都在拟合的曲线上,就像下图所示。
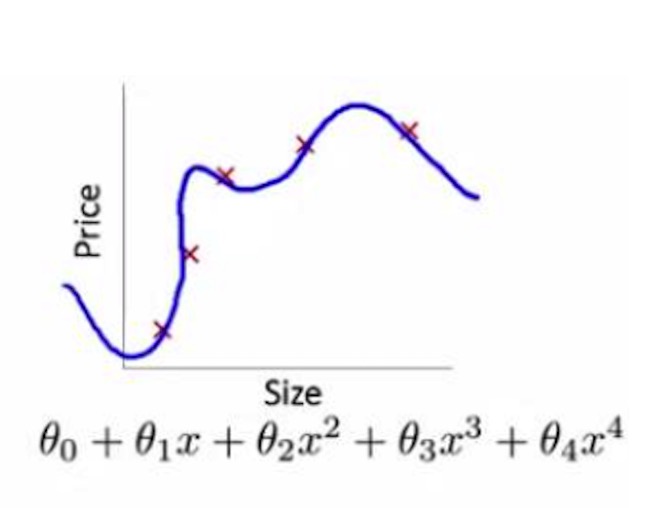
我们可以看出和二次曲线相比,该图像的其斜率较大。由于自变量的阶数对斜率的影响较小,从而可以推断出斜率变大的主要起因是权重值过大。所以减轻过拟合现象就要控制权重值不能过大,这也是为什么要加上正则项。
第二点就是目前接触到的教材都是告诉我们正则有这样几种方法,但是并没有深究这种方法的理论来源。其实正则项推导和贝叶斯学派有一定的关系,但是我比较疑惑的是添加正则项后的模型效果更好,是否说明贝叶斯学派的理论相比频率学派更优呢?关于如何从贝叶斯学派的理论推导出正则项之后再单开一篇博客进行介绍。