第三周的课程内容包括单隐层神经网络、如何初始化参数、正向传播、计算导数、梯度下降和反向传播,ng结合简单的两层深度学习模型详细阐述了深度学习的原理,中间的计算过程十分重要,需要大家耐心理解、推导。
神经元
“神经元”是深度学习网络中的最基本的单元,其结构如下图所示:
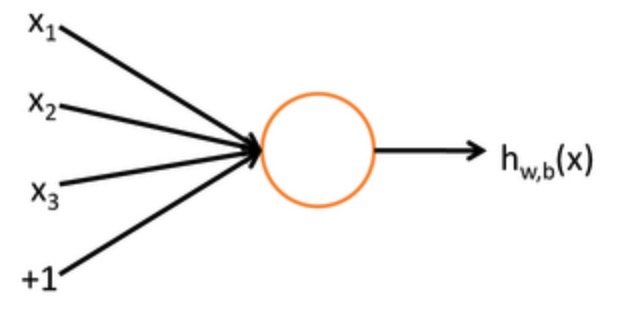
该神经元以$x_{1},x_{2},x_{3}$和截距+1为输入,各分量对应的权重值为$\omega_{1},\omega_{2},\omega_{3},b$,所以该神经元对应的输出为$h_{W,b}(x)=f\left(W^TX \right)=f(\sum_{i=1}^{3}\omega_{i}x_{i}+b)$,其中f为被称为激活函数,可以认为是sigmoid函数,后面会介绍更多的激活函数。不难看出这样的一个神经元输入输出的映射关系正是之前推导过的逻辑回归。
两层神经网络
很多简单的神经元可以构成一张复杂的神经网络,为了方便演示神经网络的工作过程,我们以两层神经网络为例进行分析。两层神经网络的结构如下图所示:
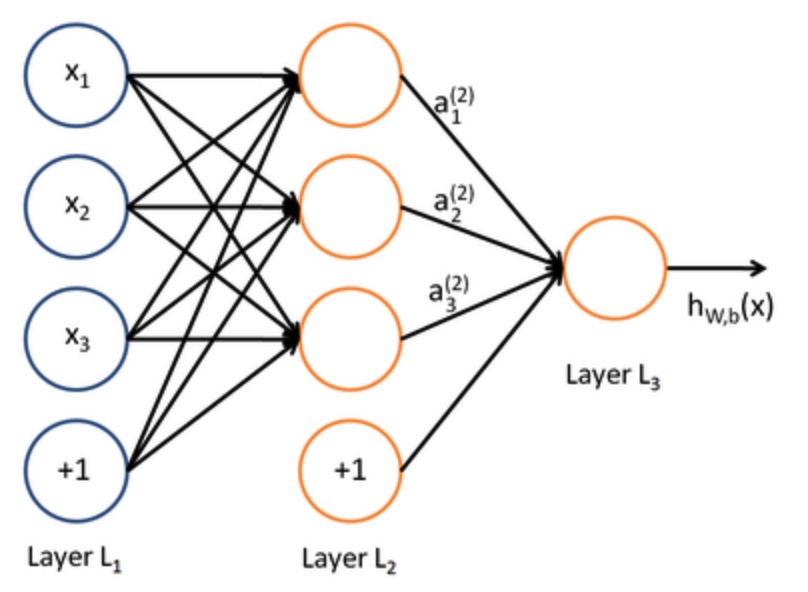
其中最左侧的是输入层,最右边的是输出层,中间的叫做隐含层,一般在说神经网络的层数时不算输入层,所以该模型是两层神经网络。该模型只包含一个隐含层,计算上较为简单,后面会根据该模型进行正向传播的推导。
正向传播
根据两层神经网络的示意图进行正向传播的推导。首先假设$n_{l}$表示网络的层数,第l层记为$L_{l}$,所以本例中$L_{1}$是输入层,$L_{2}$是隐含层,$L_{3}$是输出层。
神经网络参数主要有$\left(W,b\right)$,其中$W^{(l)}_{ij}$表示第l层第j个单元和l+1层第i个单元之间的连接参数,即权重。$b^{(l)}_{i}$是第l+1层第i个单元的偏置项。
$a^{(l)}_{i}$表示第l层第i个单元的输出值。当l=1时,$a^{(1)}_{i}=x_{i}$,也就是第i个节点的输入值。最终的输出结果用$h_{W,b}(x)$表示。
所以该神经网络的正向传播过程如下。第一层到第二层的传播过程:
$$a^{(2)}_{1}=f\left[W^{(1)}_{11} x_{1}+W^{(1)}_{12} x_{2}+W^{(1)}_{13} x_{3}+b^{(1)}_{1}\right]$$
$$a^{(2)}_{2}=f\left[W^{(1)}_{21} x_{1}+W^{(1)}_{22} x_{2}+W^{(1)}_{23} x_{3}+b^{(1)}_{2}\right]$$
$$a^{(2)}_{3}=f\left[W^{(1)}_{31} x_{1}+W^{(1)}_{32} x_{2}+W^{(1)}_{33} x_{3}+b^{(1)}_{3}\right]$$
第二层到第三层的传播过程
$$a^{(3)}_{1}=f\left[W^{(2)}_{11} a^{(2)}_{1}+W^{(2)}_{12} a^{(2)}_{2}+W^{(2)}_{13} a^{(2)}_{3}+b^{(2)}_{1}\right]$$
$$h_{W,b}(x)=a^{(3)}_{1}$$
我们用$z^{l}_{i}$表示第l层第i单元的输入加权和,例如$z^{(2)}_{i}=\sum_{j=1}^{n}W^{(1)}_{ij}x_{j}+b^{(1)}_{i}$,则$a^{(l)}_{i}=f[z^{(l)}_{i}]$,则上述传播过程可以简化为
$$z^{(2)}=W^{(1)}x+b^{(1)}$$
$$a^{(2)}=f[z^{(2)}]$$
$$z^{(3)}=W^{(2)}a^{(2)}+b^{(2)}$$
$$h_{W,b}(x)=a^{(3)}=f[z^{(3)}]$$
上面的计算过程即为神经网络的正向传播过程。
反向传播
正向传播计算出输出值$h_{W,b}(x)$后,根据与目标值$t$的误差,进行反向传播调整权重$W$和偏置$b$的值。根据平方和误差函数,针对第$p$个输入样本有$E=\frac{1}{2}\left|\left| h_{W,b} - t\right|\right|^2$,则总误差为$E_{N} = \frac{1}{N}\sum^{N}_{p=1}E_{p}$。误差从输出层反向传播,各层权重通过梯度下降算法进行更新,即$$w=w-\eta*\Delta E_{p}(w)$$其中,$\eta$是每次更新时的步长,$\Delta E_{p}(w)$是第$p$个样本的误差对某一层权重的偏导数。在这里以单输出两层神经网络为例,给出反向传播算法推导过程,为了简化公式,只考虑一个样本的情况。
对$w^{(1)}_{11},w^{(2)}_{11}$的推导。首先看第三层,输入是$z^{(3)}$,输出为$a^{(3)}$,误差为$E=\frac{1}{2}\left|\left|t - a^{(3)}\right|\right|^2$,有
$$\frac{\partial{E}}{\partial{w^{2}_{11}}}={\frac{\partial{E}}{\partial{z^{(3)}}}}{\frac{\partial{z^{(3)}}}{\partial{w^{(2)}_{11}}}}$$
对于${\frac{\partial{z^{(3)}}}{\partial{w^{(2)}_{11}}}}$,有
$${\frac{\partial{z^{(3)}}}{\partial{w^{(2)}_{11}}}}=a^{(2)}_{1}$$
对于${\frac{\partial{E}}{\partial{z^{(3)}}}}$,有
$${\frac{\partial{E}}{\partial{z^{(3)}}}} = {\frac{\partial{E}}{\partial{a^{(3)}}}}{\frac{\partial{a^{(3)}}}{\partial{z^{(3)}}}}=-(t-a^{(3)})*f’(z^{(3)})$$
若激活函数为simgoid函数,有
$${\frac{\partial{E}}{\partial{z^{(3)}}}} = -(t-a^{(3)})z^{(3)}(1-z^{(3)})$$
该结果在推导前一层权重$w$时会用到,令$\delta_{3}={\frac{\partial{E}}{\partial{z^{(3)}}}}$,代入$\frac{\partial{E}}{\partial{w^{2}_{11}}}$,有
$$\frac{\partial{E}}{\partial{w^{2}_{11}}} = \delta_{3}*a^{(2)}_{1}$$
对于第二层,需要求$\frac{\partial{E}}{\partial{w^{(1)}_{11}}}$,有
$$\frac{\partial{E}}{\partial{w^{(1)}_{11}}} = \frac{\partial{E}}{\partial{z^{(2)}_{1}}}\frac{\partial{z^{(2)}_{1}}}{\partial{w^{(1)}_{11}}}$$
其中
$$\frac{\partial{z^{(2)}_{1}}}{\partial{w^{(1)}_{11}}} = x_{1}$$
由于第三层只有一个节点,所以有
$$\frac{\partial{E}}{\partial{z^{(2)}_{1}}}= \frac{\partial{E}}{\partial{z^{(3)}_{1}}}\frac{\partial{z^{(3)}_{1}}}{\partial{z^{(2)}_{1}}}=\delta_{3}\frac{\partial{z^{(3)}_{1}}}{\partial{a^{(2)}_{1}}}\frac{\partial{a^{(2)}_{1}}}{\partial{z^{(2)}_{1}}}=\delta_{3}w^{(2)}_{11}z^{(2)}_{1}(1-z^{(2)}_{1})$$
令$\delta_{2}=\frac{\partial{E}}{\partial{z^{(2)}_{1}}}$,则有
$$\frac{\partial{E}}{\partial{w^{(1)}_{11}}}=\delta_{2}*x_{1}$$
其他的权重值与上述推导一致。
激活函数
激活函数的目的在于引入非线性,将输出映射到不同的空间。如果激活函数是线性的,那么多层次的神经网络和单层神经网络是等价的。比较常见的激活函数有simgoid函数、tanh函数、ReLU函数等。
sigmoid函数
sigmoid函数在logistic回归推导中给出了其函数图像及表达式,这里不再赘述。其优点在于能将输出映射在[0,1]区间,单调并连续。其缺点在于输入超过一定区间,函数的导数趋近于0,容易出现问题,并且其输出均值不为0.
tanh函数
tanh函数被定义为$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$,其函数图像如下所示
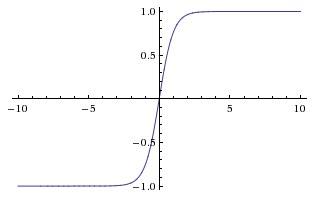
tanh函数相对于sigmoid函数来说,收敛速度更快,并且输出以0为中心,但是其依然没有解决梯度消失的问题。
ReLU函数
RuLU的定义为$y=max(0,x)$,对应的函数图像为
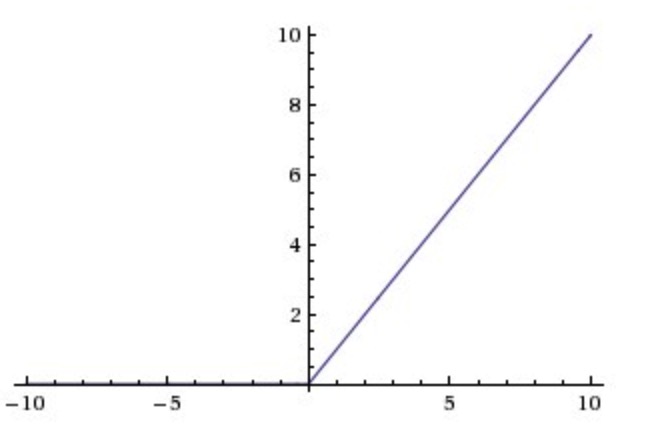
relu函数可以取得较好的结果,在实际应用中也有很多类似的变种函数。relu函数有效缓解了梯度消失的问题,计算方面也比较容易。后面遇到例子时,再详细说明各种激活函数的效果。
小结
第三周的课程比较基础,通过两层神经网络结构进行了正向、反向传播推导,简单阐述了神经网络的工作原理,然而两层网络只是比较特殊的情况,推导不具有代表性,下一章深层网络将进行普适性的推导。